
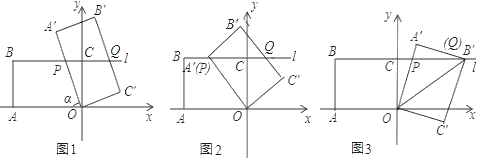
【题目】如图1,在平面直角坐标系中,O为坐标原点,点A(﹣4,0),直线l∥x轴,交y轴于点C(0,3),点B(﹣4,3)在直线l上,将矩形OABC绕点O按顺时针方向旋转α度,得到矩形OA′B′C′,此时直线OA′、B′C′分别与直线l相交于点P、Q.
(1)当α=90°时,点B′的坐标为 .
(2)如图2,当点A′落在l上时,点P的坐标为 ;
(3)如图3,当矩形OA′B′C′的顶点B′落在l上时.
①求OP的长度;②S△OPB′的值是 .
(4)在矩形OABC旋转的过程中(旋转角0°<α≤180°),以O,P,B′,Q为顶点的四边形能否成为平行四边形?如果能,请直接写出点B′和点P的坐标;如果不能,请简要说明理由.
【答案】(1)(3,4);(2)(﹣![]() ,3);(3)①OP=
,3);(3)①OP=![]() ;②
;②![]() ;(4)在矩形OABC旋转的过程中(旋转角0°<α≤180°),以O,P,B′,Q为顶点的四边形能成为平行四边形,此时点B′的坐标为(5,0),点P的坐标为(4,3).
;(4)在矩形OABC旋转的过程中(旋转角0°<α≤180°),以O,P,B′,Q为顶点的四边形能成为平行四边形,此时点B′的坐标为(5,0),点P的坐标为(4,3).
【解析】
(1)根据旋转的得到B′的坐标;
(2)根据在Rt△OCA′,利用勾股定理即可求解;
(3)①根据已知条件得到△CPO≌△A′PB′,设OP=x,则CP=A′P=4﹣x,在Rt△CPO中,利用OP2=OC2+CP2,即x2=(4﹣x)2+32即可求出x的值,即可求解;②根据S△OPB′=![]() PB′OC即可求解;
PB′OC即可求解;
(4)当点B′落在x轴上时,由OB′∥PQ,OP∥B′Q,此时四边形OPQB′为平行四边形,再根据平行四边形的性质即可求解.
解:(1)∵A(﹣4,0),B(﹣4,3),
∴OA=4,AB=3.
由旋转的性质,可知:OA′=OA=4,A′B′=AB=3,
∴当α=90°时,点B′的坐标为(3,4).
故答案为:(3,4).
(2)在Rt△OCA′中,OA′=4,OC=3,
∴A′C=![]() =
=![]() ,
,
∴当点A′落在l上时,点P的坐标为(﹣![]() ,3).
,3).
故答案为:(﹣![]() ,3).
,3).
(3)①当四边形OA′B′C′的顶点B′落在BC的延长线上时,
在△CPO和△A′PB′中,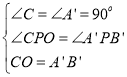 ,
,
∴△CPO≌△A′PB′(AAS),
∴OP=B′P,CP=A′P.
设OP=x,则CP=A′P=4﹣x.
在Rt△CPO中,OP=x,CP=4﹣x,OC=3,
∴OP2=OC2+CP2,即x2=(4﹣x)2+32,
解得:x=![]() ,
,
∴OP=![]() .
.
②∵B′P=OP=![]() ,
,
∴S△OPB′=![]() PB′OC=
PB′OC=![]() ×
×![]() ×3=
×3=![]() .
.
故答案为:![]() .
.
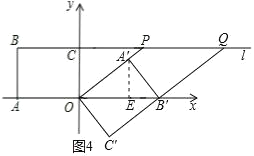
(4)当点B′落在x轴上时,∵OB′∥PQ,OP∥B′Q,
∴此时四边形OPQB′为平行四边形.
过点A′作A′E⊥x轴于点E,如图4所示.
∵OA′=4,A′B′=3,
∴OB′=![]() =5,A′E=
=5,A′E=![]() =
=![]() ,OE=
,OE=![]() =
=![]() ,
,
∴点B′的坐标为(5,0),点A′的坐标为(![]() ,
,![]() ).
).
设直线OA′的解析式为y=kx(k≠0),
将A′(![]() ,
,![]() )代入y=kx,得:
)代入y=kx,得:
![]() =
=![]() k,解得:k=
k,解得:k=![]() ,
,
∴直线OA′的解析式为y=![]() x.
x.
当y=3时,有![]() x=3,
x=3,
解得:x=4,
∴点P的坐标为(4,3).
∴在矩形OABC旋转的过程中(旋转角0°<α≤180°),以O,P,B′,Q为顶点的四边形能成为平行四边形,此时点B′的坐标为(5,0),点P的坐标为(4,3).


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案科目:初中数学 来源: 题型:
【题目】“十·一”黄金周期间,武汉动物园在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
人数变化单位:万人 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(1)若9月30日的游客人数记为![]() ,请用
,请用![]() 的代数式表示10月2日的游客人数?
的代数式表示10月2日的游客人数?
(2)请判断七天内游客人数最多的是哪天?请说明理由。
(3)若9月30日的游客人数为2万人,门票每人10元。问黄金周期间武汉动物园门票收入是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在研究位似问题时,甲、乙同学的说法如下:
甲:如图①,已知矩形ABCD和矩形EFGO在平面直角坐标系中,点B,F的坐标分别为(﹣4,4),(2,1).若矩形ABCD和矩形EFGO是位似图形,点P(点P在GC上)是位似中心,则点P的坐标为(0,2).
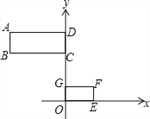
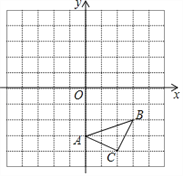
图① 图②
乙:如图②,正方形网格中,每个小正方形的边长是1个单位长度,以点C为位似中心,在网格中画△A1B1C1,使△A1B1C1与△ABC位似,且△A1B1C1与△ABC的位似比为2:1,则点B1的坐标为(4,0).
对于两人的观点,下列说法正确的是( )
A. 两人都对 B. 两人都不对 C. 甲对乙不对 D. 甲不对乙对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,已知点O,A的坐标分别为(0,0),(﹣3,﹣2).
(1)点B的坐标是 ,点B与点A的位置关系是 .现将点B,点A都向右平移5个单位长度分别得到对应点C和D,顺次连接点A,B,C,D,画出四边形ABCD;
(2)横、纵坐标都是整数的点成为整数点,在四边形ABCD内部(不包括边界)的整数点M使S△ABM=8,请直接写出所有点M的可能坐标;
(3)若一条经过点(0,﹣4)的直线把四边形ABCD的面积等分,则这条直线的表达式是 ,并在图中画出这条直线.
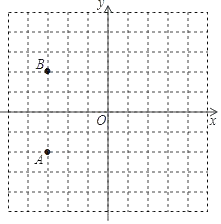
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,为美化校园环境,某校计划在一块长为20m,宽为15m的长方形空地上修建一条宽为a(m)的甬道,余下的部分铺设草坪建成绿地.
(1)甬道的面积为 m2,绿地的面积为 m2(用含a的代数式表示);
(2)已知某公园公司修建甬道,绿地的造价W1(元),W2(元)与修建面积S之间的函数关系如图2所示.①园林公司修建一平方米的甬道,绿地的造价分别为 元, 元.②直接写出修建甬道的造价W1(元),修建绿地的造价W2(元)与a(m)的关系式;③如果学校决定由该公司承建此项目,并要求修建的甬道宽度不少于2m且不超过5m,那么甬道宽为多少时,修建的甬道和绿地的总造价最低,最低总造价为多少元?
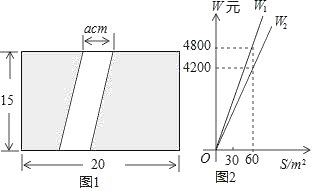
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一组数![]() ,-
,-![]() ,
,![]() ,-
,-![]() ,…,
,…,![]() (从左往右数,第1个数是
(从左往右数,第1个数是![]() ,第2个数是-
,第2个数是-![]() ,第3个数是
,第3个数是![]() ,第4个数是-
,第4个数是-![]() ,依此类推,第n个数是
,依此类推,第n个数是![]() ).
).
(1)分别写出第5个、第6个数;
(2)记这组数的前n个数的和是sn,如:
s1=![]() (可表示为1+
(可表示为1+![]() );
);
s2=![]() +(-
+(-![]() )=
)=![]() (可表示为1-
(可表示为1-![]() );
);
s 3=![]() +(-
+(-![]() )+
)+![]() =
=![]() (可表示为1+
(可表示为1+![]() );
);
s4=![]() +(-
+(-![]() )+
)+![]() +(-
+(-![]() )=
)=![]() (可表示为1-
(可表示为1-![]() ).
).
请计算S99的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一条笔直的公路依次经过A,B,C三地,且A,B两地相距1000m,B,C两地相距2000m.甲、乙两人骑车分别从A,B两地同时出发前往C地.
(1)若甲每分钟比乙多骑100m,且甲、乙同时到达C地 ,求甲的速度;
(2)若出发5 min,甲还未骑到B地,且此时甲、乙两人相距不到650m,请判断谁先到达C地,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱.各种品牌的山地车相继投放市场.顺风车行经营的![]() 型车2018年6月份销售总额为
型车2018年6月份销售总额为![]() 万元,今年经过改造升级后
万元,今年经过改造升级后![]() 型车每辆销售价比去年增加
型车每辆销售价比去年增加![]() 元,若今年6月份与去年6月份卖出的
元,若今年6月份与去年6月份卖出的![]() 型车数量相同,则今年6月份
型车数量相同,则今年6月份![]() 型车销售总额将比去年6月份销售总额增加
型车销售总额将比去年6月份销售总额增加![]() .
.
(1)今年6月份![]() 型车每辆售价多少元?(用列方程的方法解答)
型车每辆售价多少元?(用列方程的方法解答)
(2)已知![]() 两种型号车今年的进货及销售价格如下表:
两种型号车今年的进货及销售价格如下表:
|
| |
进货价格(元/辆) |
|
|
销售价格(元/辆) | 今年的销售价格 |
|
该车行计划7月份进这批![]() 型车和
型车和![]() 型车共
型车共![]() 辆,且
辆,且![]() 型车的进货数量不超过
型车的进货数量不超过![]() 型车数量的两倍,应如何进货才能是这批车获利最多?
型车数量的两倍,应如何进货才能是这批车获利最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com