
����Ŀ����ʮ��һ���ƽ����ڼ䣬�人������7�������ÿ�����ε������仯���±���������ʾ��ǰһ����������������ʾ��ǰһ���ٵ�������
���� | 10��1�� | 10��2�� | 10��3�� | 10��4�� | 10��5�� | 10��6�� | 10��7�� |
�����仯��λ������ | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
��1����9��30�յ��ο�������Ϊ![]() ������
������![]() �Ĵ���ʽ��ʾ10��2�յ��ο�������
�Ĵ���ʽ��ʾ10��2�յ��ο�������
��2�����ж��������ο��������������죿��˵�����ɡ�
��3����9��30�յ��ο�����Ϊ2���ˣ���Ʊÿ��10Ԫ���ʻƽ����ڼ��人������Ʊ�����Ƕ���Ԫ��
���𰸡���1��![]() ��2��10��3�� ��3��272����Ԫ��
��2��10��3�� ��3��272����Ԫ��
��������
��1��10��2�յ��ο�����=a+1.6+0.8��
��2���ֱ���a�Ĵ���ʽ��ʾ�������ο����������ҳ������������Լ���Ӧ�����ڼ��ɣ�
��3���Ȱ��������ο������ֱ���a�Ĵ���ʽ��ʾ������ͣ���a=2���뻯����ʽ�ӣ�����80���ɵûƽ����ڼ�ù���Ʊ�����룮
��1��a+2.4��
��2���������ο������ֱ���a+1.6��a+2.4��a+2.8��a+2.4��a+1.6��a+1.8��a+0.6��
����3������࣮
��3����a+1.6��+��a+2.4��+��a+2.8��+��a+2.4��+��a+1.6��+��a+1.8��+��a+0.6��=7a+13.2�����ˣ�����a=2ʱ��7a+13.2=27.2�����ˣ���
�ࡰʮһ���ڼ�����������Ա��ʪ�ع�����������27.2 ��10000 ��10=2720000=2.72��106��Ԫ����272����Ԫ��


 ��������ϵ�д�
��������ϵ�д� ��ӡ�Ļ���ʱ����ϵ�д�
��ӡ�Ļ���ʱ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
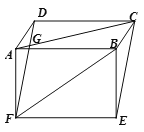
����Ŀ����֪����ͼ����ƽ���ı���ABCD�;���ABEF�У�AC��DF�ཻ�ڵ�G.
(1) ��˵��DF��CE��
(2) ��AC��BF��DF�����ACE�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ������⣺
���壺���һ������ƽ�����ک�1����Ϊi2=��1�������i����������λ����ô����a+bi��a��bΪʵ���������ͽ���������a�����������ʵ����b��������������鲿�����ļӣ������˷���������ʽ�ļӣ������˷��������ƣ�������㣺��2+i��+��3��4i��=5��3i��
��1����գ�i3=�� ����2i4=�� ����
��2�����㣺�٣�2+i����2��i����
�ڣ�2+i��2��
��3��������������ȣ������ǵ�ʵ�����鲿����ֱ���ȣ�����������⣺��֪����x+3y��+3i=��1��x����yi����x��yΪʵ��������x��y��ֵ��
��4����һ�ԣ��������i2=��1��һ֪ʶ�㣬��m2+25��mΪʵ������ʽ�ֽ�����������Ļ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
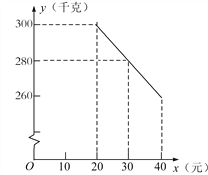
����Ŀ����ݮ�����϶��ʢ����һ��ˮ��������ijˮ�����۵��ڲ�ݮ���������������۳ɱ�Ϊÿǧ��20Ԫ�IJ�ݮ���涨�����ڼ����۵��۲����ڳɱ����ۣ�Ҳ������ÿǧ��40Ԫ�����������֣�������y(ǧ��)�����۵���x(Ԫ)����һ�κ�����ϵ����ͼ��y��x�ĺ�����ϵͼ��
(1)��y��x�ĺ�������ʽ��
(2)���ˮ�����۵�������ݮ��õ�����ΪWԪ����W�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ϣ������ɸ���ȫ��ͬ��С������ѳɵ�һ��������![]() ����ͼ��ʾ.
����ͼ��ʾ.

��1���뻭�����������![]() ������ͼ.
������ͼ.
��2�������˼�����![]() �ı������Ϻ��ᣨ���������ϵ�һ�治�磩�������������Ǻ�ɫ��С��������_______��.
�ı������Ϻ��ᣨ���������ϵ�һ�治�磩�������������Ǻ�ɫ��С��������_______��.
��3�������������ͷ����һЩ��ͬ��С������������ڼ�����![]() �ϣ�Ҫ��������ͼ������ͼ���䣬������������________��С������.
�ϣ�Ҫ��������ͼ������ͼ���䣬������������________��С������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1����AB=CD��AD=BC��OΪAC�е㣬��O���ֱ�߷ֱ���AD��BC�ཻ�ڵ�M��N����ô��1����2��ʲô��ϵ����˵�����ɣ�
����O���ֱ����ת��ͼ��2������3��������������������䣬��ôͼ��1���е���1����2�Ĺ�ϵ��������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ������������������������ij��ѧ���꼶ÿ���ѡ��5��ѧ�����һ�������ӣ�����ѧ��ʦ����֯�½���һ��֪ʶ���������������ǣ�ÿ�Ӷ�����ش�50���⣬���һ���4�֣��������һ���1�֣�
��1��������꼶һ����������÷�Ϊ190�֣���ô���꼶һ������ӻش���˶��ٵ��⣿
��2�����꼶��������ӵ����÷��п���Ϊ142������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������ABCD�У�AB=4cm����P�ӵ�D������DA���A�����˶����ٶ���1cm/s��ͬʱ����Q�ӵ�A������AB�������B�����˶����ٶ���2cm/s������PQ��CP��CQ�����˶�ʱ��Ϊt��s����0��t��2��
��1���Ƿ����ijһʱ��t��ʹ��PQ��BD�������ڣ����tֵ���������ڣ�˵������
��2������PQC�����Ϊs��cm2������s��t֮��ĺ�����ϵʽ��
��3����ͼ2������AC�����߶�PQ�ཻ�ڵ�M���Ƿ����ijһʱ��t��ʹS��QCM��S��PCM=3��5�������ڣ����tֵ���������ڣ�˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
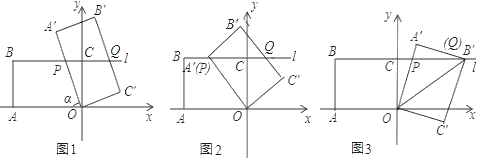
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��A����4��0����ֱ��l��x�ᣬ��y���ڵ�C��0��3������B����4��3����ֱ��l�ϣ�������OABC�Ƶ�O��˳ʱ�뷽����ת���ȣ��õ�����OA��B��C������ʱֱ��OA����B��C���ֱ���ֱ��l�ཻ�ڵ�P��Q��
��1��������90��ʱ����B��������Ϊ�� ����
��2����ͼ2������A������l��ʱ����P������Ϊ�� ����
��3����ͼ3��������OA��B��C���Ķ���B������l��ʱ��
����OP�ij��ȣ���S��OPB����ֵ���� ����
��4���ھ���OABC��ת�Ĺ����У���ת��0��������180��������O��P��B����QΪ������ı����ܷ��Ϊƽ���ı��Σ�����ܣ���ֱ��д����B���͵�P�����ꣻ������ܣ����Ҫ˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com