
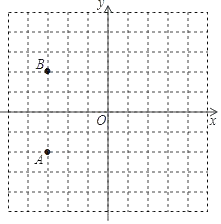
【题目】如图,在直角坐标系中,已知点O,A的坐标分别为(0,0),(﹣3,﹣2).
(1)点B的坐标是 ,点B与点A的位置关系是 .现将点B,点A都向右平移5个单位长度分别得到对应点C和D,顺次连接点A,B,C,D,画出四边形ABCD;
(2)横、纵坐标都是整数的点成为整数点,在四边形ABCD内部(不包括边界)的整数点M使S△ABM=8,请直接写出所有点M的可能坐标;
(3)若一条经过点(0,﹣4)的直线把四边形ABCD的面积等分,则这条直线的表达式是 ,并在图中画出这条直线.
【答案】(1)(﹣3,2),关于x轴对称;(2)点M(1,1),(1,0),(1,﹣1);(3)y=﹣8x﹣4
【解析】
(1)根据直角坐标系的特点即可求解,根据题意平移坐标再连接即可;
(2)设△ABM的AB边上的高为h,根据面积求出h,即可求解;
解:(1)B(﹣3,2),A、B关于x轴对称;四边形ABCD如图所示;
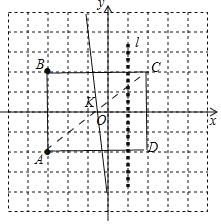
故答案为(﹣3,2),关于x轴对称.
(2)设△ABM的AB边上的高为h,由题意:![]() ×4×h=8,
×4×h=8,
∴h=4,
∴满足条件的点在直线l上,且在矩形内部,
∴点M(1,1),(1,0),(1,﹣1).
(3)∵直线把四边形ABCD的面积等分,
∴直线经过矩形的对称中心(﹣![]() ,0),
,0),
设直线的解析式为y=kx+b,则有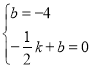 ,
,
解得![]() ,
,
∴直线的解析式为y=﹣8x﹣4.
故答案为y=﹣8x﹣4.


 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
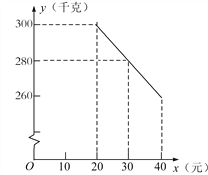
【题目】草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
(1)求y与x的函数解析式;
(2)设该水果销售店试销草莓获得的利润为W元,求W的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD中,AB=4cm,点P从点D出发沿DA向点A匀速运动,速度是1cm/s,同时,点Q从点A出发沿AB方向,向点B匀速运动,速度是2cm/s,连接PQ、CP、CQ,设运动时间为t(s)(0<t<2)
(1)是否存在某一时刻t,使得PQ∥BD?若存在,求出t值;若不存在,说明理由
(2)设△PQC的面积为s(cm2),求s与t之间的函数关系式;
(3)如图2,连接AC,与线段PQ相交于点M,是否存在某一时刻t,使S△QCM:S△PCM=3:5?若存在,求出t值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组织了“热爱宪法,捍卫宪法”的知识竞赛,赛后发现所有学生的成绩(总分100分)均不低于50分,为了解本次竞赛的成绩分布情况,随机抽取若干名学生的成绩作为样本进行整理,并绘制了不完整的统计图表,请你根据统计图表解答下列问题.
学校若干名学生成绩分布统计表
分数段(成绩为x分) | 频数 | 频率 |
50≤x<60 | 16 | 0.08 |
60≤x<70 | a | 0.31 |
70≤x<80 | 72 | 0.36 |
80≤x<90 | c | d |
90≤x≤100 | 12 | b |
(1)此次抽样调查的样本容量是 ;
(2)写出表中的a= ,b= ,c= ;
(3)补全学生成绩分布直方图;
(4)比赛按照分数由高到低共设置一、二、三等奖,若有25%的参赛学生能获得一等奖,则一等奖的分数线是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般地,任何一个无限循环小数都可以写成分数形式,现以无限循环小数0.![]() 为例进行讨论:设0.
为例进行讨论:设0.![]() =x,由0.
=x,由0.![]() =0.777…可知,10x﹣x=7.
=0.777…可知,10x﹣x=7.![]() ﹣0.
﹣0.![]() =7,即10x﹣x=7.解方程,得x=
=7,即10x﹣x=7.解方程,得x=![]() .于是,得0.
.于是,得0. ![]() =
= ![]() .则0.
.则0.![]() =____________;0.
=____________;0.![]()
![]() =____________ .
=____________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
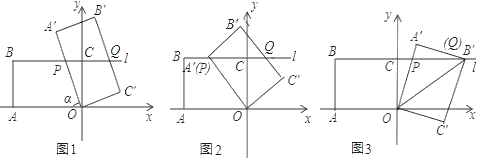
【题目】如图1,在平面直角坐标系中,O为坐标原点,点A(﹣4,0),直线l∥x轴,交y轴于点C(0,3),点B(﹣4,3)在直线l上,将矩形OABC绕点O按顺时针方向旋转α度,得到矩形OA′B′C′,此时直线OA′、B′C′分别与直线l相交于点P、Q.
(1)当α=90°时,点B′的坐标为 .
(2)如图2,当点A′落在l上时,点P的坐标为 ;
(3)如图3,当矩形OA′B′C′的顶点B′落在l上时.
①求OP的长度;②S△OPB′的值是 .
(4)在矩形OABC旋转的过程中(旋转角0°<α≤180°),以O,P,B′,Q为顶点的四边形能否成为平行四边形?如果能,请直接写出点B′和点P的坐标;如果不能,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
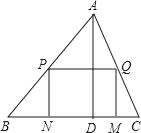
【题目】一块材料的形状是锐角三角形ABC,边BC=12cm,高AD=8cm,把它加工成矩形零件如图,要使矩形的一边在BC上,其余两个顶点分别在AB,AC上.且矩形的长与宽的比为3:2,求这个矩形零件的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:求1+2+22+23+…+22017+22018的值
解:设S=1+2+22+23+…+22017+22018,将等式两边同时乘以2得:2S=2+22+23+…+22017+22018+22019,
将下式减去上式得2S﹣S=22019﹣1,即S=22019﹣1
请你根据材料中的方法计算下列各式:
(1)1+2+22+23+…+299+2100
(2)1+![]() +
+![]() +…+
+…+![]()
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com