
【题目】一条笔直的公路依次经过A,B,C三地,且A,B两地相距1000m,B,C两地相距2000m.甲、乙两人骑车分别从A,B两地同时出发前往C地.
(1)若甲每分钟比乙多骑100m,且甲、乙同时到达C地 ,求甲的速度;
(2)若出发5 min,甲还未骑到B地,且此时甲、乙两人相距不到650m,请判断谁先到达C地,并说明理由.
【答案】(1)甲的速度为300m/min;(2)甲先到达C地.
【解析】
(1)根据题意找出等量关系,列出方程求解即可
(2)设甲的速度为x m /min,乙的速度为ym /min,根据题中条件,判断x与y的大小关系以及t甲,t乙的大小关系.
(1)设甲的速度为x m /min,则乙的速度为(x-100)m /min,由题意得
![]()
解得x=300 .
经检验,x=300是原方程的解.
答:甲的速度为300 m /min .
(2)解法一:
设甲的速度为x m /min,乙的速度为ym /min,
因为出发5 min,甲还未骑到B地,可得5x<1000,
解得x<200.
因为出发5 min,甲、乙两人相距不到650 m,可得
5y+1000—5x<650.
化简得x—y>70.
设甲、乙从出发到到达C地所用的时间分别为t甲,t乙,则
t甲—t乙=![]()
=1000(![]() ).
).
因为x—y>70,所以y<x—70.
所以3y—2x<3(x—70)—2x.
即3y—2x<x—210.
又因为x<200,
所以3y—2x<0.
因为由实际意义可知xy>0,
所以t甲—t乙<0.
即t甲<t乙 .
所以甲先到达C地.
解法二:
设甲的速度为x m /min,乙的速度为ym /min,
因为出发5 min,甲还未骑到B地,可得5x<1000,
解得x<200.
因为出发5 min,甲、乙两人相距不到650 m,可得
5y+1000—5x<650.
化简得x—y>70.
由题可知,出发后,甲经过![]() min追上乙,则此时
min追上乙,则此时
s甲=![]() .
.
因为x—y>70,且x<200,
所以s甲<![]() <3000.
<3000.
也即甲追上乙时,两人还未到达C地.
因为x>y,
所以甲先到达C地.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD中,AB=4cm,点P从点D出发沿DA向点A匀速运动,速度是1cm/s,同时,点Q从点A出发沿AB方向,向点B匀速运动,速度是2cm/s,连接PQ、CP、CQ,设运动时间为t(s)(0<t<2)
(1)是否存在某一时刻t,使得PQ∥BD?若存在,求出t值;若不存在,说明理由
(2)设△PQC的面积为s(cm2),求s与t之间的函数关系式;
(3)如图2,连接AC,与线段PQ相交于点M,是否存在某一时刻t,使S△QCM:S△PCM=3:5?若存在,求出t值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
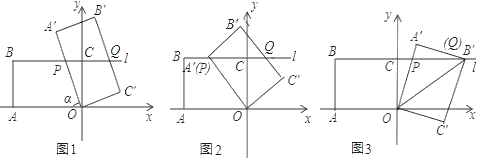
【题目】如图1,在平面直角坐标系中,O为坐标原点,点A(﹣4,0),直线l∥x轴,交y轴于点C(0,3),点B(﹣4,3)在直线l上,将矩形OABC绕点O按顺时针方向旋转α度,得到矩形OA′B′C′,此时直线OA′、B′C′分别与直线l相交于点P、Q.
(1)当α=90°时,点B′的坐标为 .
(2)如图2,当点A′落在l上时,点P的坐标为 ;
(3)如图3,当矩形OA′B′C′的顶点B′落在l上时.
①求OP的长度;②S△OPB′的值是 .
(4)在矩形OABC旋转的过程中(旋转角0°<α≤180°),以O,P,B′,Q为顶点的四边形能否成为平行四边形?如果能,请直接写出点B′和点P的坐标;如果不能,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
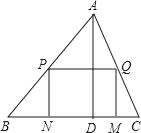
【题目】一块材料的形状是锐角三角形ABC,边BC=12cm,高AD=8cm,把它加工成矩形零件如图,要使矩形的一边在BC上,其余两个顶点分别在AB,AC上.且矩形的长与宽的比为3:2,求这个矩形零件的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
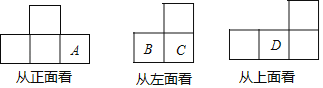
【题目】一个几何体由大小相同的小立方体搭成,从三个方向看到的几何体的形状图如图所示.
(1)求A,B,C,D这4个方格位置上的小立方体的个数;
(2)这个几何体是由多少块小立方体组成的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).

(1)请根据题中已有的信息补全频数分布表和频数分布直方图;

(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户?
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,求抽取出的2个家庭来自不同范围的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有A、B、C三点,点A和点B间距20个单位长度且点A、B表示的有理数互为相反数,AC=36,数轴上有一动点P从点A出发,以每秒1个单位长度的速度沿数轴向终点C移动,设移动时间为t秒.
![]()
(1)点A表示的有理数是 ,点B表示的有理数是 ,点C表示的有理数是 .
(2)当点P运动到点B时,点Q从点O出发,以每秒6个单位长度的速度沿数轴在点O和点C之间往复运动.
①求t为何值时,点Q第一次与点P重合?
②当点P运动到点C时,点Q的运动停止,求此时点Q一共运动了多少个单位长度,并求出此时点Q在数轴上所表示的有理数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:求1+2+22+23+…+22017+22018的值
解:设S=1+2+22+23+…+22017+22018,将等式两边同时乘以2得:2S=2+22+23+…+22017+22018+22019,
将下式减去上式得2S﹣S=22019﹣1,即S=22019﹣1
请你根据材料中的方法计算下列各式:
(1)1+2+22+23+…+299+2100
(2)1+![]() +
+![]() +…+
+…+![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①若![]() 则
则![]() 为负数;②若关于的方程
为负数;②若关于的方程![]() 有无数解,则a=b;③若
有无数解,则a=b;③若![]() ,则关于
,则关于![]() 的方程
的方程![]() 的解为
的解为![]() ;④若
;④若![]() 则
则![]() ;⑥若
;⑥若![]() ,且
,且![]() ,则
,则![]() 一定是为程
一定是为程![]() 的解;其中结论正确个数有( )
的解;其中结论正确个数有( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com