
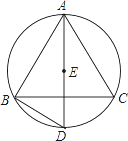
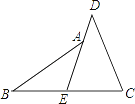
【题目】如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D.
(1)当△ABC的外接圆半径为1时,且∠BAC=60°,求弧BC的长度.
(2)连接BD,求证:DE=DB.
【答案】(1)![]() (2)详见解析.
(2)详见解析.
【解析】
(1)设△ABC的外接圆的圆心为O,连接OB、OC,由圆周角定理得出∠BOC=120°,再由弧长公式即可得出结果;
(2)连接BE,由三角形的内心得出∠1=∠2,∠3=∠4,再由三角形的外角性质和圆周角定理得出∠DEB=∠DBE,即可得出结论.
(1)解:设△ABC的外接圆的圆心为O,连接OB、OC,如图1所示:
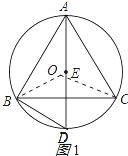
∵∠BAC=60°,
∴∠BOC=120°,
∴弧BC的长度=![]() =
=![]() .
.
(2)证明:连接BE,如图2所示:
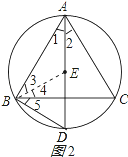
∵E是△ABC的内心,
∴∠1=∠2,∠3=∠4,
∵∠DEB=∠1+∠3,∠DBE=∠4+∠5
∠5=∠2,
∴∠DEB=∠DBE,
∴DE=DB.


科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线,与边BC交于点E,若AD=![]() , AC=3.则DE长为( )
, AC=3.则DE长为( )
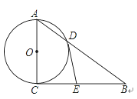
A. ![]() B. 2 C.
B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲班56人,其中身高在160厘米以上的男同学10人,身高在160厘米以上的女同学3人,乙班80人,其中身高在160厘米以上的男同学20人,身高在160厘米以上的女同学8人.如果想在两个班的160厘米以上的女生中抽出一个作为旗手,在哪个班成功的机会大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B为定点,定直线l//AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:①线段MN的长;②△PMN的面积;③△PAB的周长;④∠APB的大小;⑤直线MN,AB之间的距离.其中会随点P的移动而不改变的是( )

A. ①②③ B. ①②⑤ C. ②③④ D. ②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的题目及分析过程,并按要求进行证明.已知:如图,E是BC的中点,点A在DE上,且∠BAE=∠CDE.
求证:AB=CD.
证明两条线段相等,常用的一般方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要证明的两条线段,它们不在同一个三角形中,且它们分别所在的两个三角形也不全等.因此,要证AB=CD,必须添加适当的辅助线,构造全等三角形或等腰三角形.
现给出如下三种添加辅助线的方法,请任意选择其中一种,对原题进行证明.
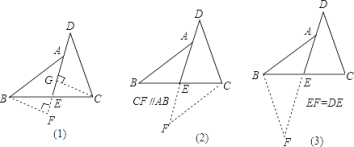
查看答案和解析>>
科目:初中数学 来源: 题型:
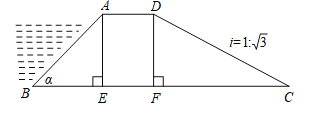
【题目】如图所示,某拦水大坝的横断面为梯形ABCD,AE、DF为梯形的高,其中迎水坡AB的坡角α=45°,坡长AB=![]() 米,背水坡CD的坡度i=1:
米,背水坡CD的坡度i=1:![]() (i为DF与FC的比值),则背水坡CD的坡长为______米.
(i为DF与FC的比值),则背水坡CD的坡长为______米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果精确到0.1米)
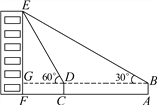
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上,老师为了解女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.

(1)求女生进球数的平均数、中位数;
(2)投球4次,进球3个以上(含3个)为优秀,全校有女生1200人,估计为“优秀”等级的女生约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
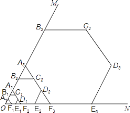
【题目】如图,∠MON=60°,作边长为1的正六边形A1B1C1D1E1F1,边A1B1、F1E1分别在射线OM、ON上,边C1D1所在的直线分别交OM、ON于点A2、F2, 以A2F2为边作正六边形A2B2C2D2E2F2, 边C2D2所在的直线分别交OM、ON于点A3、F3, 再以A3F3为边作正六边形A3B3C3D3E3F3, …,依此规律,经第4次作图后,点B4到ON的距离是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com