
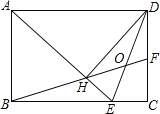
【题目】如图,在矩形ABCD中,AD=![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②AB=HF,③BH=HF;④BC﹣CF=2HE;⑤OE=OD;其中正确结论的序号是_____________
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②AB=HF,③BH=HF;④BC﹣CF=2HE;⑤OE=OD;其中正确结论的序号是_____________
【答案】①③⑤
【解析】分析:①根据角平分线的定义可得∠BAE=∠DAE=45°,然后利用求出△ABE是等腰直角三角形,根据等腰直角三角形的性质可得AE=![]() AB,从而得到AE=AD,然后利用“角角边”证明△ABE和△AHD全等,根据全等三角形对应边相等可得BE=DH,再根据等腰三角形两底角相等求出∠ADE=∠AED=67.5°,根据平角等于180°求出
AB,从而得到AE=AD,然后利用“角角边”证明△ABE和△AHD全等,根据全等三角形对应边相等可得BE=DH,再根据等腰三角形两底角相等求出∠ADE=∠AED=67.5°,根据平角等于180°求出
∠CED=67.5°,从而判断出①正确;
②判断出△ABH不是等边三角形,从而得到AB≠BH,即AB≠HF,得到②错误.
③求出∠EBH=∠OHD=22.5°,∠AEB=∠HDF=45°,然后利用“角边角”证明△BEH和△HDF全等,根据全等三角形对应边相等可得BH=HF,判断出③正确;
④根据全等三角形对应边相等可得DF=HE,然后根据HE=AE-AH=BC-CD,BC-CF=BC-(CD-DF)=2HE,判断出④正确;
⑤求出∠AHB=67.5°,∠DHO=∠ODH=22.5°,然后根据等角对等边可得OE=OD=OH,判断出⑤正确;
解析:∵在矩形ABCD中,AE平分∠BAD,∴∠BAE=∠DAE=45°,∴△ABE是等腰直角三角形,∴AE=![]() AB,∵AD=
AB,∵AD=![]() AB,∴AE=AD,
AB,∴AE=AD,
在△ABE和△AHD中,
{ | ∠BAE=∠DAE ∠ABE=∠AHD=90° AE=AD |
∴△ABE≌△AHD(AAS),
∴BE=DH,∴AB=BE=AH=HD,∴∠ADE=∠AED=![]()
∴∠CED=180°-45°-67.5°=67.5°,∴∠AED=∠CED,故①正确;
∵AB=AH,∠BAE=45°,∴△ABH不是等边三角形,∴AB≠BH,∴即AB≠HF,故②错误;
∵∠EBH=90°-67.5°=22.5°,∴∠EBH=∠OHD,
在△BEH和△HDF中,
{ | ∠EBH=∠OHD=22.5° BE=DH ∠AEB=∠HDF=45° |
∴△BEH≌△HDF(ASA),∴BH=HF,HE=DF,故③正确;
∵HE=AE-AH=BC-CD,∴BC-CF=BC-(CD-DF)=BC-(CD-HE)=(BC-CD)+HE=HE+HE=2HE.故④正确;
∵AB=AH,∵∠AHB=![]() ∠OHE=∠AHB(对顶角相等),
∠OHE=∠AHB(对顶角相等),
∴∠OHE=67.5°=∠AED,∴OE=OH,∵∠DHO=90°-67.5°=22.5°,∠ODH=67.5°-45°=22.5°,∴∠DHO=∠ODH,∴OH=OD,∴OE=OD=OH,故⑤正确;
综上所述,结论正确的是①③④⑤共4个.
故答案为①③④⑤.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
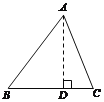
【题目】在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
思路:(1) 作AD⊥BC于D,设BD = x,用含x的代数式表示CD;(2)根据勾股定理,利用AD作为“桥梁”,建立方程模型,求出x;(3)利用勾股定理求出AD的长,再计算三角形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
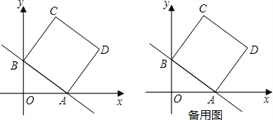
【题目】如图,在平面直角坐标系中,直线y=﹣![]() 分别与x轴、y轴交于点A、B,且点A的坐标为(8,0),四边形ABCD是正方形.
分别与x轴、y轴交于点A、B,且点A的坐标为(8,0),四边形ABCD是正方形.
(1)填空:b= ;
(2)点D的坐标为 ;
(3)点M是线段AB上的一个动点(点A、B除外),在x轴上方是否存在另一个点N,使得以O、B、M、N为顶点的四边形是菱形?若不存在,请说明理由;若存在,请求出点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,高速公路旁有一个测速站M到公路l的距离MN为60米,一辆小汽车在公路l上行驶,测得此车从点A行驶到点B所有的时间为3秒,已知∠MAN=30°,∠MBN=60°.
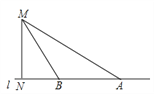
(1)计算此车从A到B的平均速度为每秒多少米(结果保留整数);
(2)若此高速公路限速80千米/时,判断此车是否超速.(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com