
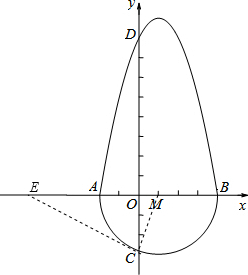
 定义:把一个半圆与抛物线的一部分合成封闭图形,我们把这个封闭图形称为“蛋圆”.如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,A,B,C,D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,8),AB为半圆的直径,半圆的圆心M的坐标为(1,0),半圆半径为3.
定义:把一个半圆与抛物线的一部分合成封闭图形,我们把这个封闭图形称为“蛋圆”.如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,A,B,C,D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,8),AB为半圆的直径,半圆的圆心M的坐标为(1,0),半圆半径为3.
|
|
| OE |
| OC |
| OC |
| OM |
| 32-12 |
| 2 |
| OC2 |
| OM |
(2
| ||
| 1 |
|


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
| 数量x(张) | 单价(元/张) |
| x≤100 | 40 |
| 100<x≤200 | 前100张,单价40,超过部分单价打9折 |
| 200<x≤500 | 前100张,单价40,超过部分单价打8折 |
| x>500 | 前100张,单价40,超过部分单价打7折 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 幼儿园购买了一个板长AB 4m,支架OC高0.8m的翘翘板,支点O在板AB的中点.因支架过高不宜小朋友玩,故把它暂时存放在高2.4m的车库里,准备改装.现有几个小朋友把板的一端A按到地面上.
幼儿园购买了一个板长AB 4m,支架OC高0.8m的翘翘板,支点O在板AB的中点.因支架过高不宜小朋友玩,故把它暂时存放在高2.4m的车库里,准备改装.现有几个小朋友把板的一端A按到地面上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com