练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．因式分解：
    （1）ax+ay；
    （2）3mx-6my；
    （3）8m2n+2mn；
    （4）12xyz-9x2y2；
    （5）p（a2+b2）-q（a2+b2）；
    （6）4a2（x+7）-3（x+7）．

    分析 （1）直接提取公因式a，进而分解因式即可；
    （2）直接提取公因式3m，进而分解因式即可；
    （3）直接提取公因式2mn，进而分解因式即可；
    （4）直接提取公因式3xy，进而分解因式即可；
    （5）直接提取公因式a2+b2，进而分解因式即可；
    （6）直接提取公因式x+7，进而分解因式即可．

    解答 解：（1）ax+ay=a（x+y）；

    （2）3mx-6my=3m（x-2y）；

    （3）8m2n+2mn=2mn（4m+1）；

    （4）12xyz-9x2y2=3xy（4z-3xy）；

    （5）p（a2+b2）-q（a2+b2）=（a2+b2）（p-q）；

    （6）4a2（x+7）-3（x+7）=（x+7）（4a2-3）．

    点评 此题主要考查了提取公因式法分解因式，正确找出公因式是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    11．如图1，二次函数的图象与y轴交于点C（0，2），与x轴的正半轴交于点E（6，0），直线CB∥x轴，与抛物线交于点B，点B的横坐标为4，过点B作BA⊥x轴于点A，点P是线段上一点，把射线CP沿直线BC翻折，交射线AB于点M．
    （1）求二次函数的表达式及抛物线的对称轴；
    （2）设OP=m，求△PCM的面积，并观察计算结果，你发现什么规律？
    （3）如图2，当点P与点E重合时，直线CB与MP交于点Q，将△POC以每秒1个单位的速度沿x轴正方向平移，直到点O与点E（P）重合时停止，设运动的时间为t，平移后的△O1C1P1与△CEM的重叠部分的面积为S，求S与t之间的函数表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．已知O、G、H分别是△ABC的外心、重心、垂心，AF是中线，AD⊥BC于D，BE⊥AC于E，求证：O、G、H三点共线，且GH=2OG．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．求下列各数的算术平方根及平方根．
    （1）64；
    （2）0.25；
    （3）$\frac{4}{9}$；
    （4）56；
    （5）（-$\frac{4}{13}$）2；
    （6）104．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如果球的半径是r，则球的体积用公式V=$\frac{4}{3}$πr3来计算，当体积V=500cm3，半径r是多少厘米？（π取3.14，精确到0.01cm）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．计算：
    （1）（$\sqrt{4}$）2=4；
    （2）（$\sqrt{3}$）2=3’
    （3）$\sqrt{（\frac{3}{4}）^{2}}$=$\frac{3}{4}$；
    （4）$\sqrt{（-2）^{2}}$=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．计算：
    （1）6$\frac{3}{5}$+24-18+4$\frac{4}{5}$-16+18-6.8-3.2
    （2）-（+0.5）-（-3$\frac{1}{4}$）+2.75-（+7$\frac{1}{2}$）
    （3）|-7$\frac{3}{8}$+4$\frac{1}{2}$|+（-18$\frac{1}{4}$）+|-6-$\frac{1}{2}$|
    （4）（-4$\frac{1}{8}$）-|-1+2+0.125|-|-3$\frac{1}{3}$|-（-6$\frac{1}{7}$）+（-5$\frac{1}{7}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．解方程：3x（x-3）=2（x-1）（x+1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

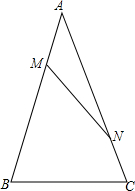    10．如图，已知△ABC中，AB=AC，AM=CN，探求：∠ABC与∠ANM满足∠B-∠ANM=30°时，$\frac{MN}{BC}$=$\frac{\sqrt{3}}{3}$．

    查看答案和解析>>

    同步练习册答案