Question

11．如图1，二次函数的图象与y轴交于点C（0，2），与x轴的正半轴交于点E（6，0），直线CB∥x轴，与抛物线交于点B，点B的横坐标为4，过点B作BA⊥x轴于点A，点P是线段上一点，把射线CP沿直线BC翻折，交射线AB于点M．
（1）求二次函数的表达式及抛物线的对称轴；
（2）设OP=m，求△PCM的面积，并观察计算结果，你发现什么规律？
（3）如图2，当点P与点E重合时，直线CB与MP交于点Q，将△POC以每秒1个单位的速度沿x轴正方向平移，直到点O与点E（P）重合时停止，设运动的时间为t，平移后的△O₁C₁P₁与△CEM的重叠部分的面积为S，求S与t之间的函数表达式．

Answer 1

分析 （1）设所求二次函数的解析式为y=ax²+bx+c（a≠0），再把点C（0，2）代入求出c的值，求出B（4，2），E（6，0）代入解析式得出A、B的值，进而可得出结论；
（2）过点M作MN⊥OC于点N，设PC与AB交于点G，由对称性可得BM=BG，由相似三角形的判定定理得出△APG∽△BCG，再根据相似三角形的性质得出BM=BG=$\frac{8}{m}$，由S_△PCM=S_梯形OPMN-S_△OPC-S_△CMN即可得出结论；
（3）由（3）知，当点P与点E重合时，BM=$\frac{4}{3}$，M（4，$\frac{10}{3}$），根据BQ∥AE得出△MBQ∽△MAE，故可得出CQ的长．
①当0≤t＜$\frac{24}{5}$时，设C₁O₁与CP交于点F，C₁P₁交ME于点H，由相似三角形的判定定理得出△C₁QH∽△P₁EH．根据相似三角形对应高的比等于相似比可设△P₁EH边EP₁上的高为h，则△C₁QH边C₁Q上的高为2-h，故可得出$\frac{5}{12}$t，S_△P1EH=$\frac{5}{24}$t²．再由S=S_?C1CEP1-S_△P1EH-S_△CC1F即可得出结论；
②当$\frac{24}{5}$≤t＜6时，设C₁O₁与ME交于点K，与CE交于点R，同理可得△C₁QK∽△EO₁R，故O₁K=10-$\frac{5}{3}$t，S_△O1EK=$\frac{5}{6}$t²-10t+30．在Rt△RO₁E中根据S=S_△O1EK-S_△O1ER即可得出结论．

解答 解：（1）设所求二次函数的解析式为y=ax²+bx+c（a≠0），
∵二次函数的图象与y轴交于点C（0，2），
∴c=2．
∵CB∥x轴，
∴B（4，2）．
∵B（4，2），E（6，0），
∴$\left\{\begin{array}{l}0=36a+6b+2\\ 2=16a+4b+2\end{array}\right.$，解得$\left\{\begin{array}{l}a=-\frac{1}{6}\\ b=\frac{2}{3}\end{array}\right.$，
∴二次函数的解析式为y=-$\frac{1}{6}$x²+$\frac{2}{3}$x+2，即y=-$\frac{1}{6}$（x-2）²+$\frac{8}{3}$，
∴抛物线的对称轴为直线x=2；

（2）如图1，过点M作MN⊥OC于点N，设PC与AB交于点G，由对称性可得BM=BG．
∵OA=BC=4，AB=OC=2，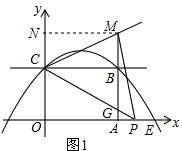
∴AP=m-4．
∵∠CBG=∠PAG，∠BGC=∠AGP，
∴△APG∽△BCG，
∴$\frac{AP}{BC}$=$\frac{AG}{BG}$，即$\frac{m-4}{4}$=$\frac{2-BG}{BG}$，
∴BM=BG=$\frac{8}{m}$，
∴M（4，2+$\frac{8}{m}$）．
∵S_△PCM=S_梯形OPMN-S_△OPC-S_△CMN=$\frac{1}{2}$（4+m）（2+$\frac{8}{m}$）-$\frac{1}{2}$×2m-$\frac{1}{2}$×$\frac{8}{m}$×4=8，
∴△PCM的面积与m无关，即点P在线段AE上运动时，△PCM的面积不变；

（3）由（3）知，当点P与点E重合时，BM=$\frac{4}{3}$，M（4，$\frac{10}{3}$），
∵BQ∥AE，
∴△MBQ∽△MAE，
∴$\frac{MB}{MA}$=$\frac{BQ}{AE}$，即$\frac{\frac{4}{3}}{\frac{10}{3}}$=$\frac{BQ}{2}$，
∴BQ=$\frac{4}{5}$，
∴CQ=BC+BQ=4+$\frac{4}{5}$=$\frac{24}{5}$．
①当0≤t＜$\frac{24}{5}$时，如图2，设C₁O₁与CP交于点F，C₁P₁交ME于点H，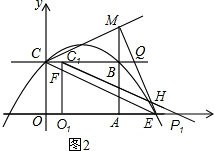
∵CC₁=t，
∴C₁O=$\frac{24}{5}$-t，EP₁=t．
∵OP∥BC，
∴△C₁QH∽△P₁EH．
∵相似三角形对应高的比等于相似比，
∴设△P₁EH边EP₁上的高为h，则△C₁QH边C₁Q上的高为2-h，
∴$\frac{h}{2-h}$=$\frac{t}{\frac{24}{5}-t}$，解得h=$\frac{5}{12}$t，
∴S_△P1EH=$\frac{1}{2}$EP₁•h=$\frac{1}{2}$t•$\frac{5}{12}$t=$\frac{5}{24}$t²．
∵∠ECB=∠CEO，
∴tan∠BCM=tan∠CEO=$\frac{2}{6}$=$\frac{1}{3}$．
在Rt△CC₁F中，
∵CF=CC₁•tan∠EAB=$\frac{1}{3}$t，
∴S_△CC1F=$\frac{1}{2}$CC₁•CF=$\frac{1}{2}$t•$\frac{1}{3}$t=$\frac{1}{6}$t²．
∴S=S_?C1CEP1-S_△P1EH-S_△CC1F=2t-$\frac{5}{24}$t²-$\frac{1}{6}$t²=-$\frac{3}{8}$t²+2t，即S=-$\frac{3}{8}$t²+2t；
②当$\frac{24}{5}$≤t＜6时，如图3，
设C1O1与ME交于点K，与CE交于点R，
∵CC₁=t，
∴C₁Q=t-$\frac{24}{5}$，O₁E=6-t，
易得△C₁QK∽△EO₁R，
∴$\frac{{C}_{1}Q}{{O}_{1}E}$=$\frac{{C}_{1}K}{{O}_{1}K}$，即$\frac{t-\frac{24}{5}}{6-t}$=$\frac{2-{O}_{1}K}{{O}_{1}K}$，解得O₁K=10-$\frac{5}{3}$t，
∴S_△O1EK=$\frac{1}{2}$EO₁•EK=$\frac{1}{2}$（6-t）（10-$\frac{5}{3}$t）=$\frac{5}{6}$t²-10t+30．
在Rt△RO₁E中，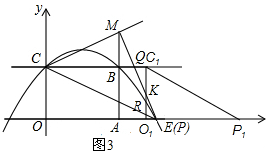
∵RO₁=EO₁•tan∠CEO=$\frac{1}{3}$（6-t），
∴S_△O1ER=$\frac{1}{2}$EO₁•RE₁=$\frac{1}{2}$（6-t）×$\frac{1}{3}$（6-t）=$\frac{1}{6}$t²-2t+6，
∴S=S_△O1EK-S_△O1ER=$\frac{5}{6}$t²-10t+30-（$\frac{1}{6}$t²-2t+6）=$\frac{2}{3}$t²-8t+24．
综上所述，S与t的函数关系式为S=$\left\{\begin{array}{l}-\frac{3}{8}{t}^{2}+2t（0≤t＜\frac{24}{5}）\\ \frac{2}{3}{t}^{2}-8t+24（\frac{24}{5}≤t＜6）\end{array}\right.$．

点评 本题考查的是二次函数综合题，涉及到相似三角形的判定与性质、利用待定系数法求二次函数的解析式、三角形的面积公式等知识，在解答（3）时要注意进行分类讨论．