解:

(1)将点(1,3)代入

(k>0),可得:3=
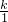
,
解得:k=3.
故k的值为3.
(2)过点E作EF⊥BC于点F,
∵点E的横坐标为3,点E在反比例函数y=

上,
∴EF=1,OF=3,
又∵四边形ABCD是矩形,
∴AB=2EF=2,即点A的纵坐标为2,
∴OB=

,
∴BF=CF=OF-OB=

,
∴OC=OF+CF=3+

=

,
即点C的横坐标为

.
(3)∵点E的横坐标为m,点E在反比例函数y=

上,
∴EF=

,OF=m,
又∵四边形ABCD是矩形,
∴AB=2EF=

,即点A的纵坐标为

,
∴OB=

,
∴BF=CF=OF-OB=m-

=

,
∴BC=m,
又∵∠ABD=45°,
∴AB=AD=BC,即

=m,
解得:m
1=

,m
2=-

(舍去).
故m的值为

.
分析:(1)将点(1,3)代入反比例函数关系式,可得出k的值;
(2)过点E作EF⊥BC于点F,根据点E的横坐标为3,可得EF=1,OF=3,由矩形的性质可得AB=2EF=2,求出OB,可得出BF、CF,继而得出点C的横坐标.
(3)根据(2)的思路求出BC的长度,由AB=BC建立方程,解出即可得出答案.
点评:本题考查了反比例函数的综合,涉及了矩形的性质、反比例函数图象上点的坐标特点、待定系数法求反比例函数解析式的知识,综合考察的知识点较多,解答本题关键是数形结合思想及方程思想的综合运用.

 如图,已知点(1,3)在函数
如图,已知点(1,3)在函数 (x>0)的图象上,矩形ABCD 的边BC在x轴上,E是对角线AC、BD的交点,函数
(x>0)的图象上,矩形ABCD 的边BC在x轴上,E是对角线AC、BD的交点,函数 (k>0)的图象又经过A、E两点,请解答下列问题:
(k>0)的图象又经过A、E两点,请解答下列问题: (1)将点(1,3)代入
(1)将点(1,3)代入 (k>0),可得:3=
(k>0),可得:3=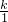 ,
, 上,
上, ,
, ,
, =
= ,
, .
. 上,
上, ,OF=m,
,OF=m, ,即点A的纵坐标为
,即点A的纵坐标为 ,
, ,
, =
= ,
, =m,
=m, ,m2=-
,m2=- (舍去).
(舍去). .
.

 如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )
如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( ) 如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设
如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设