
【题目】如图,在平面直角坐标系中,矩形OABC的顶点B的坐标为(10,4),点D是OA的中点,点P在边BC上运动,当△ODP是等腰三角形时,点P的坐标为 . 
【答案】(2,4)或(3,4)或(8,4)或(2.5,4)
【解析】解:∵B的坐标是(10,4),四边形OCBA是矩形, ∴OC=AB=4,
∵D为OA中点,
∴OD=AD=5,
∵P在BC上,
∴P点的纵坐标是4,
以O为圆心,以OD为半径作弧,交BC于P,如图1所示: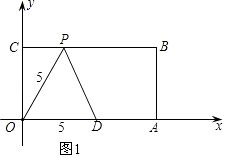
此时OP=OD=5,
由勾股定理得:CP=3,
即P的坐标是(3,4);
由勾股定理得:CP=3,
即P的坐标是(3,4);
以D为圆心,以OD为半径作弧,交BC于P、P′,如图2所示: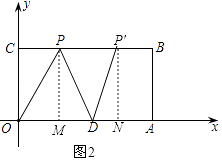
此时DP=OD=DP′=5,
由勾股定理得:DM=DN=3,
即P的坐标是(2,4),
P′的坐标是(8,4);
③作OD的垂直平分线交BC于P,如图3所示: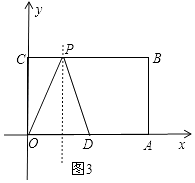
此时OP=DP,P的坐标是(2.5,4);
所以答案是:(2,4)或(3,4)或(8,4)或(2.5,4).
【考点精析】掌握等腰三角形的性质和矩形的性质是解答本题的根本,需要知道等腰三角形的两个底角相等(简称:等边对等角);矩形的四个角都是直角,矩形的对角线相等.


科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD中,AD∥BC,∠ABC=∠DCB,AB=DC。
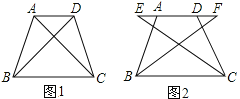
(1)求证:AC=DB;
(2)如图2,E、F两点同时从A、D出发在直线AD上以相同的速度反向而行,BF和CE会相等吗?请证明你的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】最近,“校园安全”受到全社会的广泛关注,巫溪中学对部分学生就校园安全知识的了解程度, 采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如下两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)扇形统计图中“基本了解”部分对应扇形的圆心角为 度;请补全条形统计图;
(2)若达到“了解”程度的人中有1名男生,2名女生,达到“不了解”程度的人中有1名男生和1名女生,若分别从达到“了解”程度和“不了解”程度的人中分别抽取1人参加校园知识竞赛,请用树状图或列表法求出恰好抽到1名男生和1名女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C顺时针方向旋转60°,到△ADC,连接OD.
(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由.
(3)探索:当α为多少度时,△AOD是等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com