
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C顺时针方向旋转60°,到△ADC,连接OD.
(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由.
(3)探索:当α为多少度时,△AOD是等腰三角形.
【答案】
(1)
证明:由旋转的性质得:CO=CD,∠OCD=60°,
∴△COD是等边三角形;
(2)
解:当α=150°,即∠BOC=150°时,△AOD是直角三角形.理由如下:
由旋转的性质得:△BOC≌△ADC,
∴∠ADC=∠BOC=150°,
又∵△COD是等边三角形,
∴∠ODC=60°,
∴∠ADO=90°,
即△AOD是直角三角形;
(3)
解:分三种情况:
①AO=AD时,∠AOD=∠ADO.
∵∠AOD=360°﹣∠AOB﹣∠COD﹣α=360°﹣110°﹣60°﹣α=190°﹣α,∠ADO=α﹣60°,
∴190°﹣α=α﹣60°
∴α=125°;
②OA=OD时,∠OAD=∠ADO.
∵∠AOD=190°﹣α,∠ADO=α﹣60°,
∴∠OAD=180°﹣(∠AOD+∠ADO)=50°,
∴α﹣60°=50°
∴α=110°;
③OD=AD时,∠OAD=∠AOD.
∵190°﹣α=50°
∴α=140°.
综上所述:当α的度数为125°或110°或140°时,△AOD是等腰三角形.
【解析】(1)由旋转的性质得出CO=CD,∠OCD=60°,即可得出结论;(2)由旋转的性质得出△BOC≌△ADC,得出∠ADC=∠BOC=150°,由等边三角形的性质得出∠ODC=60°,求出∠ADO=90°即可;(3)分三种情况:①AO=AD时;②OA=OD时;③OD=AD时;由等腰三角形的性质和三角形内角和定理即可求出结果.
【考点精析】利用旋转的性质对题目进行判断即可得到答案,需要熟知①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点B的坐标为(10,4),点D是OA的中点,点P在边BC上运动,当△ODP是等腰三角形时,点P的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D、E分别是边AB、AC的中点,将△ADE沿着DE对折,点A落在BC边上的点F,若∠B=50°,则∠BDF的度数为( ) 
A.50°
B.70°
C.75°
D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,点E、F分别是AD、BC的中点,分别连接BE、DF、BD.
(1)求证:△AEB≌△CFD;
(2)若四边形EBFD是菱形,求∠ABD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,地面上有一个不规则的封闭图形ABCD,为求得它的面积,小明在此封闭图形内画出一个半径为1 m的圆后,在封闭图形ABCD附近闭上眼睛向封闭图形内掷小石子(可把小石子近似看成点),
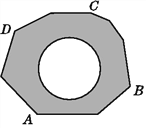
记录如下:
掷小石子所落的总次数 小石子所落的有效区域 | 50 | 150 | 300 | … |
小石子落在圆内(含圆上)的次数m | 14 | 48 | 89 | … |
小石子落在圆以外的阴影部分(含外缘)的次数n | 30 | 95 | 180 | … |
(1)当投掷的次数很大时,m∶n的值越来越接近___________(结果精确到0.1);
(2)若以小石子所落的有效区域里的次数为总数(即m+n),则随着投掷次数的增加,小石子落在圆内(含圆上)的频率稳定在___________附近;
(3)若你投一次石子,则小石子落在圆内(含圆上)的概率为___________;
(4)请你利用(2)中所得频率,估计整个封闭图形ABCD的面积是多少平方米(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学表达式:①-2<0; ②3x-5>0; ③ x=1; ④x2-x ;⑤x≠-2 ;⑥x+2>x-1中,不等式有( ).
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次体育测试中,小芳所在小组8个人的成绩分别是:46,47,48,48,49,49,49,50.则这8个人体育成绩的中位数是( )
A.47B.48C.48.5D.49
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com