练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

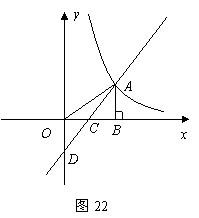
    如图22所示，在直角坐标系中，点是反比例函数的图象上一点，轴的正半轴于点，是的中点；一次函数的图象经过、两点，并将轴于点若

       （1）求反比例函数和一次函数的解析式；

       （2）观察图象，请指出在轴的右侧，当时， 的取值范围．

    解：作轴于

    ∵

    ∴

    ∴············ 1分

    ∵为的中点，

    ∴

    ∴

    ∴

    ∴···························· 2分

    将代入中，得

    ．···························· 3分

    将和代入得解之得：

    ∴··························· 4分

    （2）在轴的右侧，当时，

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    孔明是一个喜欢探究钻研的同学，他在和同学们一起研究某条抛物线y=ax2（a＜0）的性质时，将一把直角三角板的直角顶点置于平面直角坐标系的原点O，两直角边与该抛物线交于A、B两点，请解答以下问题：
    （1）若测得OA=OB=2
    		2
    （如图1），求a的值；
    （2）对同一条抛物线，孔明将三角板绕点O旋转到如图2所示位置时，过B作BF⊥x轴于点F，测得OF=1，写出此时点B的坐标，并求点A的横坐标
     
    ；
    （3）对该抛物线，孔明将三角板绕点O旋转任意角度时惊奇地发现，交点A、B的连线段总经过一个固定的点，试说明理由并求出该点的坐标．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

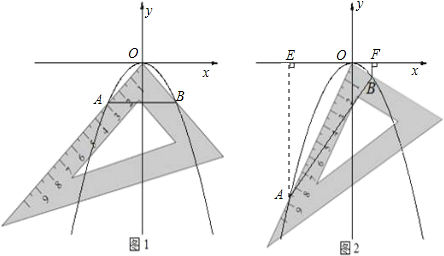
    小明将一幅三角板如图所示摆放在一起，发现只要知道其中一边的长就可以求出其它各边的长．（两个三角板分别是等腰直角三角形和含30°的直角三角形）
    若已知CD=2，求AC的长．
    请你先阅读并完成解法一，然后利用锐角三角函数的知识写出与解法一不同的解法．
    解法一：在Rt△ABC中，∵BD=CD=2 
    ∴由勾股定理，BC=
    		22+22
    =2
    		2

    在Rt△ABC中，设AB=x
    ∵∠BCA=30°，∴AC=2AB=2x
    由勾股定理，AB2+BC2=AC2，即x2+(2
    		2
    )2=(2x)2
    ∵x＞0，解得x=
    2
    		6
    3
    2
    		6
    3
    ．∴AC=
    4
    		6
    3
    4
    		6
    3
    ．
    解法二：

    查看答案和解析>>

    科目：初中数学 来源： 题型：

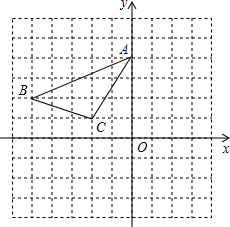    △ABC在如图所示的平面直角坐标系中，将其平移得△A1B1C1，若B的对应点B1坐标为（-3，1）．
    （1）此次平移可以看作将△ABC向右平移了
    2
    2
    个单位长度，再向下平移了
    1
    1
    个单位长度，得△A1B1C1．
    （2）在图中画出△A1B1C1．
    （3）再将△A1B1C1向右平移3个单位，向上平移两个单位，直接写出A2，B2，C2的对应点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    按要求画图并填空：
    （1）△ABC在如图1所示的平面直角坐标系中，将其平移后得△A′B′C′，若B的对应点B′的坐标是（4，1）．
    ①在图中画出△A′B′C′； 
    ②此次平移可看作将△ABC向
    左
    左
    平移了
    2
    2
    个单位长度，再向
    下
    下
    平移了
    1
    1
    个单位长度得△A′B′C′；
    ③△A′B′C′的面积为
    10
    10
    ．
    （2）已知：如图2，△ABC，请在图中作出它的角平分线BD，中线CE和BC边上的高AF．
    （3）如图3，这是一个动物园游览示意图，试建立一个适当的平面直角坐标系描述这个动物园图中每个景点位置，（画出图形，并写出各景点的坐标）． 

    查看答案和解析>>

    同步练习册答案