
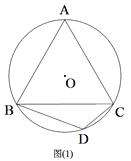
【题目】已知:△ABC是⊙O的内接三角形,且AB=BC,点D为劣弧BC上的一点,连接BD、DC.
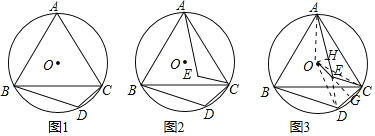
(1)如图1,若∠BDC=120°,求证:△ABC是等边三角形;
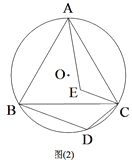
(2)如图2,在(1)的条件下,线段CD绕点C顺时针旋转60°,得到线段CE,连接AE,求证:BD=AE;
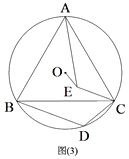
(3)如图3,在(2)的条件下,连接OE,若⊙O的半径为![]() ,OE=2,求BD的长.
,OE=2,求BD的长.
【答案】(1)见解析;(2)见解析;(3)BD=3![]() .
.
【解析】
(1)根据圆内接四边形的性质和等边三角形的判定解答即可;
(2)根据等边三角形的性质和全等三角形的判定证明即可;
(3)连接ED,利用勾股定理和直角三角形的性质解答即可.
证明:(1)∵四边形ABDC内接于⊙O,
∴∠BDC+∠BAC=180°,
∴∠BAC=180°-∠BOA=180°-120°=60°.
∵BA=BC,
∴△ABC是等边三角形.
(2)由(1)知△ABC是等边三角形,
∴∠BCA=60°,
∵∠DCE=60°,
∴∠BCA=∠DCE
而∠BCA=∠BCE+∠ECA,∠DCE=∠BCD+∠BCE,
∴∠ECA=∠DCB,
∵在△CDB与△CEA中
 ,
,
∴△CDB≌△CEA(SAS)
∴DB=AE;
(3)连接ED,可知△CDE为等边三角形,
∴∠DCE=∠DEC=∠EDC=60°,
∵∠BDC=120°
由(2)知△CDB≌△CEA,
∴∠BDC=∠AEC=120°,∠DEC+∠AEC=180°,
∴A、E、D三点在同一直线上,连接OD、OC,
 ,
,
∵OD=OC,ED=EC,
∴OE是线段DC的中垂线,
∴OE是∠DEC平分线,
设直线OE与CD的交点为G,则有∠EDG=![]() ∠DEC=30°,
∠DEC=30°,
∴∠OEA=∠DEG=30°,
连接OA,过点O作OH⊥AE,垂足为H,
在直角三角形OEH中,OE=2,∠OEA=30°,
∴OH=![]() OE=1
OE=1
可得EH=![]() ,
,
在直角三角形OAH中,OA=![]() ,OH=1,根据勾股定理,得AH=2
,OH=1,根据勾股定理,得AH=2![]() ,
,
∴AE=AH+HE=3![]() ,
,
∴BD=AE=3![]() .
.


科目:初中数学 来源: 题型:
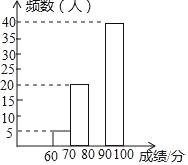
【题目】某校组织了一次全校2000名学生参加的比赛,赛后发现所有参赛学生的成绩均不低于60分,为了更好地了解本次大赛的成绩分布情况,随机抽取了100名学生的成绩(成绩x取整数,满分100分)作为样本进行整理,得到下列不完整的统计表:
请依据所给信息,解答下列问题:
(1)直接填空:a= ,b= ,c= ;
(2)请补全频数分布直方图;
(3)请自己提出一个与该题信息相关的问题,并解答你提出的问题.
成绩x/分 | 频数 | 频率 |
60≤x<70 | 5 | 0.05 |
70≤x<80 | 20 | b |
80≤x<90 | a | c |
90≤x≤100 | 40 | 0.40 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠MAN=30°,O为边AN上一点,以点O为圆心,2为半径作⊙O,交AN于D,E两点,设AD=x.
(1)如图①,当x取何值时,⊙O与AM相切?
(2)如图②,当x为何值时,⊙O与AM相交于B,C两点,且∠BOC=90°?
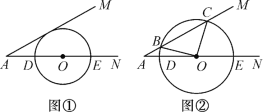
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC、BD相交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E.若AB=![]() ,BD=2,则BE的长等于_____.
,BD=2,则BE的长等于_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是从一副扑克牌中取出的两组牌,分别是黑桃1,2,3,4和方块1,2,3,4,将它们背面朝上分别重新洗牌后,从两组牌中各摸出一张,那么摸出的两张牌的牌面数字之和等于5的概率是多少?请你用列举法(列表或画树状图)加以分析说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
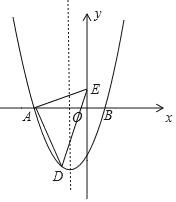
【题目】如图,在平面直角坐标系中,二次函数y=ax2+bx﹣3交x轴于点A(﹣3,0)、B(1,0),在y轴上有一点E(0,1),连接AE.
(1)求二次函数的表达式;
(2)若点D为抛物线在x轴负半轴下方的一个动点,求△ADE面积的最大值;
(3)抛物线对称轴上是否存在点P,使△AEP为等腰三角形?若存在,请直接写出所有P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为菱形ABCD对角线上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点M.
(1)求证:CD与⊙O相切;
(2)若菱形ABCD的边长为2,∠ABC=60°,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
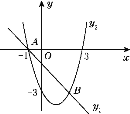
【题目】如图,A(-1,0),B(2,-3)两点在一次函数y=-x+m与二次函数y=ax2+bx-3的图象上.
(1)求m的值和二次函数的表达式;
(2)设二次函数的图象交y轴于点C,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com