
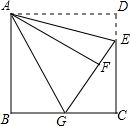
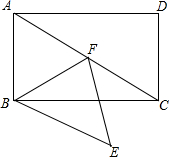
 已知:如图,四边形ABCD为正方形,E为CD边上的一点,连接AE,并以AE为对称轴,作与△ADE成轴对称的图形△AFE,延长EF(或FE)交直线BC于G.
已知:如图,四边形ABCD为正方形,E为CD边上的一点,连接AE,并以AE为对称轴,作与△ADE成轴对称的图形△AFE,延长EF(或FE)交直线BC于G.分析 (1)根据折叠的性质,△ADE≌△AGE,得到AD=AF=AB,DE=FE,∠DAE=∠FAE,∠D=∠AFE=∠AFG=90°=∠B,然后根据“HL”可证明Rt△ABG≌Rt△AFG,则GB=GF,∠BAG=∠FAG,所以∠GAE=$\frac{1}{2}$∠BAD=45°;GE=GF+EF=BG+DE;
(2)AB=1,GF=m,FE=n,则EG、CG、CE可以用m、n表示,由于∠C=90°,根据勾股定理列方程即可解答;
(3)不成立,此时,EF=BF-DE,∠EAF=45°成立,证明方法与(1)类似.
解答 解:如图1,∵把△ADE沿AE折叠使△ADE落在△AFE的位置,
∴△ADE≌△AGE
∴AD=AF=AB,DE=FE,∠DAE=∠FAE,∠D=∠AFE=∠AFG=90°=∠B,
在Rt△ABG和Rt△AFG中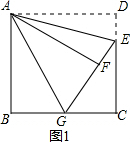 ,
,
$\left\{\begin{array}{l}{AB=AF}\\{AG=AG}\end{array}\right.$,
∴Rt△ABG≌Rt△AFG(HL),
∴GB=GF,∠BAG=∠FAG,
∴∠GAE=∠FAE+∠FAG=$\frac{1}{2}$∠BAD=45°,
∴GE=GF+EF=BG+DE;
(2)如图1,设AB=1,GF=m,FE=n,则EG=m+n,CG=1-m,CE=1-n,
∵∠C=90°,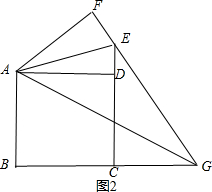
∴(1-m)2+(1-n)2=(m+n)2,
整理得:m+n+mn=1;
(3)EF=BF+DE不成立,
理由:如图2,此时,EF=BF-DE,∠EAF=45°成立.
同(1)有△ADE≌△AGE,Rt△ABG≌Rt△AFG,
∴DE=FE,GB=GF,∠DAE=∠FAE,∠BAG=∠FAG,
∴GE=GF-EF=BG-DE,
∠GAE=∠FAG-∠FAE=$\frac{1}{2}$∠BAD=45°.
点评 本题主要考查了翻折变换、全等三角形的判定与性质、勾股定理等知识的综合运用,发现图形中△ADE≌△AGE以及Rt△ABG≌Rt△AFG,是解决问题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
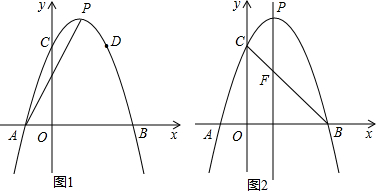
 如图,点F在?ABCD的对角线AC上,过点F、B分别作AB、AC的平行线相交于点E,连接BF,∠ABF=∠FBC+∠FCB.
如图,点F在?ABCD的对角线AC上,过点F、B分别作AB、AC的平行线相交于点E,连接BF,∠ABF=∠FBC+∠FCB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查一沓钞票中有没有假钞 | B. | 调查我市中学生课外阅读的时间 | ||
| C. | 调查本市居民的年人均消费 | D. | 调查某种灯泡的使用寿命 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=1,b=$\frac{1}{4}$ | B. | a=1,b=-$\frac{1}{4}$ | C. | a=0,b=-$\frac{1}{2}$ | D. | a=2,b=$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com