练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．如图，在矩形ABCD中，点E为AD的中点，请只用无刻度的直尺作图
    （1）如图1，在BC上找点F，使点F是BC的中点；
    （2）如图2，在AC上取两点P，Q，使P，Q是AC的三等分点．

    分析 （1）根据矩形的对角线相等且互相平分作出图形即可；
    （2）根据矩形的性质和三角形中位线定理作出图形即可．

    解答 解：（1）如图1，连接AC、BD交于点O，
    延长EO交BC于F，
    则点F即为所求；
    （2）如图2，BD交AC于O，延长EO交BC于F，
    连接EB交AC于P，连接DF交AC于Q，
    则P、Q即为所求．

    点评 本题考查的是作图的应用，掌握矩形的性质和三角形中位线定理、正确作出图形是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

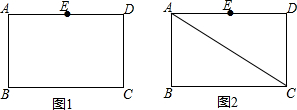
    2．已知A，B两地相距400千米，章老师驾车以80千米/小时的速度从A地到B地．汽车出发前油箱中有油25升，途中加油若干升，已知油箱中剩余油量y（升）与行驶时间t（小时）之间的关系如下图所示．假设汽车每小时耗油量保持不变，以下说法错误的是（　　）
    A．加油前油箱中剩余油量y（升）与行驶时间t（小时）的函数关系是y=-8t+25
    B．途中加油21升
    C．汽车加油后还可行驶4小时
    D．汽车到达B地时油箱中还余油6升

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．计算：20150+|$\sqrt{3}$-1|-（$\frac{1}{2}$）-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

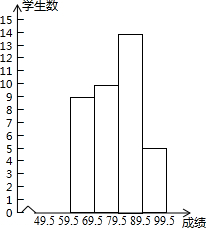    20．某班九年级（1）班40名学生期中考试的数学成绩（满分：100分）如下：
     63849153 69 81 61 69 91 78 
     75 81 8067  7681  7994  6169 
     89 70 70 87 81 86 90 88 85 67
     71 82 87 7587  9553  6574  77
    徐老师按10分的组距分段，算出每个分数段学生成绩出现的频数，填入频数分布表：
     成绩表49.5～59.5  59.5～69.569.5～79.5 79.5～89.5 89.5～99.5 
     频数记录  正 正正 正正 正
     频数 29  14 5 
    （1）请你把频数分布表、频数分布直方图补充完整；
    （2）请指出中位数在你哪个分数段，并求出中位数；
    （3）请你帮徐老师统计一下这次数学考试的及格率（60分以上为及格）；
    （4）如果该校九年级学生共有360名学生，估计该校九年级学生期中考试数学成绩的及格人数有多少名．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．如图，在等腰△ABC中，AD是角平分线，E是AB的中点，已知AB=AC=15cm．BC=18cm，则△ADE的周长是27cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

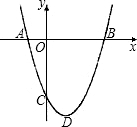    17．如图，抛物线y=$\frac{1}{2}$x2+bx+c与x轴交于A，B两点，点A的坐标为（-1，0），与y轴交于点C（0，-2）．
    （1）求抛物线的解析式及顶点D的坐标；
    （2）点M（m，0）是x轴上的一个动点，当MC+MD的值最小时，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

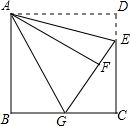    4．已知：如图，四边形ABCD为正方形，E为CD边上的一点，连接AE，并以AE为对称轴，作与△ADE成轴对称的图形△AFE，延长EF（或FE）交直线BC于G．
    （1）求证：DE+BG=EG；∠EAG=45°；
    （2）设AB=1，GF=m，FE=n，求m+n+mn的值；
    （3）若将条件中的“E为CD边上的一点”改为“E为射线CD上的一点”，则（1）中的结论还成立吗？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图，在“W”形中，AB∥CD，BC∥DE，试比较∠B与∠D的大小，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．已知：正方形ABCD，等腰直角三角板的直角顶点落在正方形的顶点C处，使三角板绕点C旋转．
    （1）当三角板旋转到图1的位置时，猜想DE与BF的数量关系，并加以证明；
    （2）在（1）的条件下，若BE：CE：DE=1：2：3，求∠BEC的度数；
    （3）若BC=2，点M是边AB的中点，连结CM，CM与BD交于点O，当三角板的一边CF与边CM重合时（如图2），若OF=$\frac{\sqrt{5}}{6}$，求DN的长．

    查看答案和解析>>

    同步练习册答案