
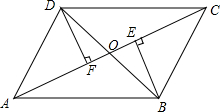
 如图,四边形ABCD的对角线AC、BD交于点O,BE⊥AC于E,DF⊥AC于F,点O既是AC的中点,又是EF的中点.
如图,四边形ABCD的对角线AC、BD交于点O,BE⊥AC于E,DF⊥AC于F,点O既是AC的中点,又是EF的中点.| 1 |
| 2 |
|
| 1 |
| 2 |


科目:初中数学 来源: 题型:
 如图所示,在长30m,宽20m的花园,要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草.要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)
如图所示,在长30m,宽20m的花园,要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草.要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com