
【题目】在![]() 中,
中,![]() ,
,
(1)如图![]() ,
,![]() 是
是![]() 上的点,过点
上的点,过点![]() 作直线截
作直线截![]() ,使截得的三角形与
,使截得的三角形与![]() 相似.例如:过点
相似.例如:过点![]() 作
作![]() 交
交![]() 于
于![]() ,则截得的
,则截得的![]() 与
与![]() 相似.请你在图中画出所有满足条件的直线.
相似.请你在图中画出所有满足条件的直线.
(2)如图![]() ,
,![]() 是
是![]() 上异于点
上异于点![]() ,
,![]() 的动点,过点
的动点,过点![]() 作直线截
作直线截![]() ,使截得的三角形与
,使截得的三角形与![]() 相似,直接写出满足条件的直线的条数.(不要求画出具体的直线)
相似,直接写出满足条件的直线的条数.(不要求画出具体的直线)
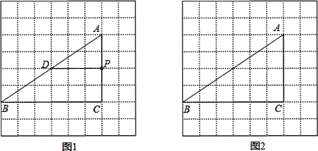
【答案】见解析
【解析】
(1)利用平行于三角形一边的直线和其他两边相交,所截得的三角形与原三角形相似的判定定理过点P作两条,再利用两组对应角相等的两个三角形相似的判定定理,过点P作两条.
(2)把Q点看成从C点出发到B点的动点,发现当Q点在某一个位置时,所作截的三角形与原三角形相似的数量减少了一个,通过此时的临界条件把QC的长度计算出来,进行分类说明.
(1)如图所示:
第一种:利用平行于三角形一边的直线和其他两边相交,所截得的三角形与原三角形相似的判定定理,过点P分别做AB与BC的平行线PD与PE.分别得到△ADP∽△ABC. △PCE∽△ACB.
第二种:利用两组对应角相等的两个三角形相似的判定定理,过P分别做PG垂直AB于点G,做PF交BC于点F,使∠PFC=∠A.分别得到△AGP∽△ACB, △FPC∽△ACB.
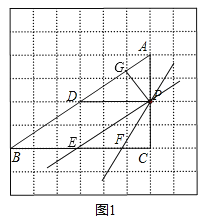
(2)
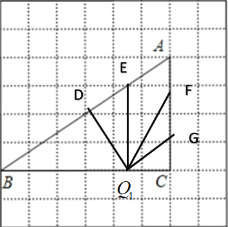
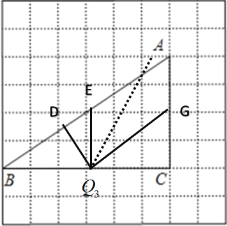
如图所示,假设点Q从点C开始往点B移动,由(1)可知,作QD⊥AB,
得△BQD∽△BAC.作QF交AC于点F,使∠QFC=∠B,得△QCF∽△ACB.
作QE∥AC,得△BQE∽△BCA.作QG∥AB,得△QCG∽△BCA.
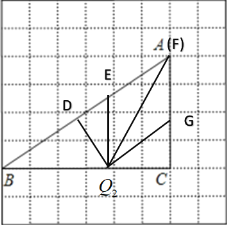
当移动到![]() 位置时,此时出现点F于点A重合,此时是一个临界点,利用△QCF∽△ACB得到
位置时,此时出现点F于点A重合,此时是一个临界点,利用△QCF∽△ACB得到![]() ,则
,则![]() 又此时CA=CF,所以QC=
又此时CA=CF,所以QC=![]()
该点往左移动,不能在三角形ABC内做出作QF交AC于点F,该点往右移动,可以在三角形ABC内做出作QF交AC于点F,使△QCF∽△ACB.
故当0<QC≤![]() 时,满足条件的直线有4条;
时,满足条件的直线有4条;
当![]() <QC<6时,满足条件的直线有3条.
<QC<6时,满足条件的直线有3条.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】(探究函数![]() 的图象与性质)
的图象与性质)
(1)函数![]() 的自变量x的取值范围是________;
的自变量x的取值范围是________;
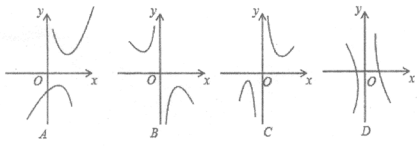
(2)下列四个函数图象中,函数![]() 的图象大致是_______;
的图象大致是_______;
(3)对于函数![]() ,求当x>0时,y的取值范围。请将下面求解此问题的过程补充完整:
,求当x>0时,y的取值范围。请将下面求解此问题的过程补充完整:
解:因为x>0,所以![]()
![]() _________。
_________。
因为![]() ,所以y________。
,所以y________。
(拓展运用)
(4)若函数![]() ,则y的取值范围是_______________________。
,则y的取值范围是_______________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为纪念“五四运动”100周年,某校举行了征文比赛,该校学生全部参加了比赛.比赛设置一等、二等、三等三个奖项,赛后该校对学生获奖情况做了抽样调查,并将所得数据绘制成如图所示的两幅不完整的统计图.根据图中信息解答下列问题:
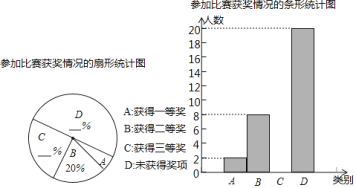
(1)本次抽样调查学生的人数为 .
(2)补全两个统计图,并求出扇形统计图中A所对应扇形圆心角的度数.
(3)若该校共有840名学生,请根据抽样调查结果估计获得三等奖的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分别求出满足下列条件的二次函数的解析式.
(1)图象经过点A(1,0),B(0,-3),对称轴是直线x=2;
(2)图象顶点坐标是(-2,3),且过点(1,-3);
(3)图象经过点(-1,3),(1, 3),(2,6).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分7分) 已知:如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=![]() OB.
OB.
(1)求证:AB是⊙O的切线;
(2)若∠ACD=45°,OC=2,求弦CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周长相等的正三角形、正四边形、正六边形的面积S3、S4、S6间的大小关系是( )
A. S3>S4>S6 B. S6>S4>S3 C. S6>S3>S4 D. S4>S6>S3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解学生“第二课堂“活动的选修情况,对报名参加A.跆拳道,B.声乐,C.足球,D.古典舞这四项选修活动的学生(每人必选且只能选修一项)进行抽样调查.并根据收集的数据绘制了图①和图②两幅不完整的统计图.
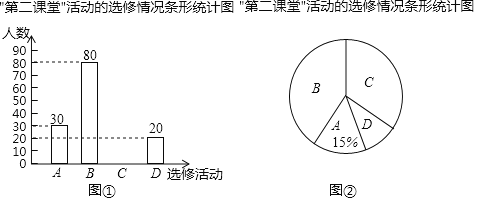
根据图中提供的信息,解答下列问题:
(1)本次调查的学生共有 人;在扇形统计图中,B所对应的扇形的圆心角的度数是 ;
(2)将条形统计图补充完整;
(3)在被调查选修古典舞的学生中有4名团员,其中有1名男生和3名女生,学校想从这4人中任选2人进行古典舞表演.请用列表或画树状图的方法求被选中的2人恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
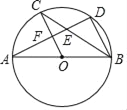
【题目】如图,AB是⊙O的直径,C、D是⊙O上的点,且OC∥BD,AD分别与BC、OC相较于点E、F,则下列结论:①AD⊥BD;②∠AOC=∠AEC; ③BC平分∠ABD;④△CEF≌△BED.其中一定成立的是_____(把你认为正确结论的序号都填上).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com