
【题目】现有5根小木棒,长度分别为:2、3、4、5、7(单位:cm),从中任意取出3根,
(1)列出所选的3根小木棒的所有可能情况;
(2)如果用这3根小木棒首尾顺次相接,求它们能搭成三角形的概率.
【答案】
(1)解:根据题意可得:所选的3根小木棒的所有可能情况为:(2、3、4),(2、3、5),(2、3、7),(2、4、5),(2、4、7),(2、5、7),(3、4、5),(3、4、7),(3、5、7),(4、5、7)
(2)解:∵能搭成三角形的结果有:(2、3、4),(2、4、5),(3、4、5),(3、5、7),(4、5、7)共5种,
∴P(能搭成三角形)= ![]() =
= ![]()
【解析】(1)首先根据题意利用列举法,即可求得所选的3根小木棒的所有可能情况;(2)利用三角形的三边关系,可求得它们能搭成三角形的共有5种情况,继而利用概率公式求解即可求得答案.
【考点精析】认真审题,首先需要了解三角形三边关系(三角形两边之和大于第三边;三角形两边之差小于第三边;不符合定理的三条线段,不能组成三角形的三边),还要掌握列表法与树状图法(当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁4名同学进行一次羽毛球单打比赛,要从中选出2名同学打第一场比赛,求下列事件的概率:
(1)已确定甲打第一场,再从其余3名同学中随机选取1名,恰好选中乙同学;
(2)随机选取2名同学,其中有乙同学.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,这样就可以求出67.5°角的正切值是( ) 
A.![]() +1
+1
B.![]() +1
+1
C.2.5
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两人分别从A(1, ![]() )、B(6,0)两点同时出发,点O为坐标原点,甲沿AO方向、乙沿BO方向均以4km/h的速度行驶,th后,甲到达M点,乙到达N点.
)、B(6,0)两点同时出发,点O为坐标原点,甲沿AO方向、乙沿BO方向均以4km/h的速度行驶,th后,甲到达M点,乙到达N点. 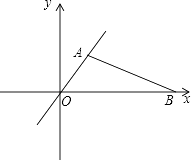
(1)请说明甲、乙两人到达O点前,MN与AB不可能平行;
(2)当t为何值时,△OMN∽△OBA;
(3)甲、乙两人之间的距离为MN的长,设s=MN2 , 求s与t之间的函数关系式,并求甲、乙两人之间距离的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实施“节能产品惠民工程”一年半以来,国家通过发放补贴的形式支持推广高效节能空调、1.6升及以下排量节能汽车、节能灯三类产品,其中推广节能汽车约120万辆,按每辆3000元标准给予一次性定额补贴.小刚同学根据了解到的信息进行统计分析,绘制出两幅不完整的统计图: 
(注:图中A表示“高效节能空调”;B表示“1.6升及以下排量节能汽车”;C表示“节能灯”)
(1)国家对上述三类产品共发放补贴金额亿元,“B”所在扇形的圆心角为°;
(2)补全条形统计图;
(3)国家计划再拿出98亿元继续推广上述三类产品.请你预测,可再推广节能汽车多少万辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知动点P在正比例函数y=x的图象上,点P的横坐标为m(m>0),以点P为圆心, ![]() m为半径的圆交x轴于A、B两点(点A在点B的左侧),交y轴于C、D两点(点D在点C的上方).点E为平行四边形DOPE的顶点(如图).
m为半径的圆交x轴于A、B两点(点A在点B的左侧),交y轴于C、D两点(点D在点C的上方).点E为平行四边形DOPE的顶点(如图). 
(1)写出点B、E的坐标(用含m的代数式表示);
(2)连接DB、BE,设△BDE的外接圆交y轴于点Q(点Q异于点D),连接EQ、BQ,试问线段BQ与线段EQ的长是否相等?为什么?
(3)连接BC,求∠DBC﹣∠DBE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校是乒乓球体育传统项目学校,为进一步推动该项目的开展,学校准备到体育用品店购买直拍球拍和横拍球拍若干副,并且每买一副球拍必须要买10个乒乓球,乒乓球的单价为2元/个,若购买20副直拍球拍和15副横拍球拍花费9000元;购买10副横拍球拍比购买5副直拍球拍多花费1600元.
(1)求两种球拍每副各多少元?
(2)若学校购买两种球拍共40副,且直拍球拍的数量不多于横拍球拍数量的3倍,请你给出一种费用最少的方案,并求出该方案所需费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com