
����Ŀ����ƽ��ֱ������ϵxOy�У���֪����P������������y=x��ͼ���ϣ���P�ĺ�����Ϊm��m��0�����Ե�PΪԲ�ģ� ![]() mΪ�뾶��Բ��x����A��B���㣨��A�ڵ�B����ࣩ����y����C��D���㣨��D�ڵ�C���Ϸ�������EΪƽ���ı���DOPE�Ķ��㣨��ͼ����
mΪ�뾶��Բ��x����A��B���㣨��A�ڵ�B����ࣩ����y����C��D���㣨��D�ڵ�C���Ϸ�������EΪƽ���ı���DOPE�Ķ��㣨��ͼ���� 
��1��д����B��E�����꣨�ú�m�Ĵ���ʽ��ʾ����
��2������DB��BE�����BDE�����Բ��y���ڵ�Q����Q���ڵ�D��������EQ��BQ�������߶�BQ���߶�EQ�ij��Ƿ���ȣ�Ϊʲô��
��3������BC�����DBC����DBE�Ķ�����
���𰸡�
��1���⣺��ͼ�٣�����PB������P��PM��x���ڵ�M��
�������֪��OM=PM=m��PB= ![]() m��
m��
��Rt��PBM�У��ɹ��ɶ����ã�
BM= ![]() =
= ![]() =2m��
=2m��
��OB=OM+BM=m+2m=3m��
��B��3m��0����
����PD������P��PN��y���ڵ�N��ͬ�������DN=2m��OD=3m��
����D��DR��PE�ڵ�R��
��ƽ���ı���DOPE�����ODE+��DOP=180�㣻
�������֪����DOP=45�㣬���ODE=135�㣬
���EDR=45�㣬����EDRΪ����ֱ�������Σ�
��ER=DR=OM=m��EM=ER+RM=ER+OD=m+3m=4m��
��E��m��4m��
��2���⣺��ȣ��������£�
�����⻭��ͼ�Σ���ͼ����ʾ��
�ɣ�1��֪����ODE=��BDO+��BDE=135�㣬
��OB=OD=3m������OBDΪ����ֱ�������Σ����BDO=45�㣬
���BDE=90�㣬����BDEΪֱ�������Σ�
��Բ�ܽǶ�����֪��BEΪ��BDE���Բ��ֱ�������BQE=90�㣮
����E��EK��y���ڵ�K������EK=m��OK=4m��
�ߡ�BQE=90�㣬���EQK+��BQO=90�㣬�֡�BQO+��QBO=90�㣬
���EQK=��QBO��
��Rt��EQK��Rt��QBO��
�� ![]() ����
���� ![]() �����OQ=m��OQ=3m��
�����OQ=m��OQ=3m��
�ߵ�Q���D���غϣ���OQ=m��
��OQ=EK�������Ʊ�Ϊ1����ʱ����������ȫ�ȣ�
��BQ=EQ
��3���⣺��ͼ����ʾ������BC��
�ɣ�1����֪����ͼ�٣�CD=2DQ=4m����OC=CD��OD=m��
�ɣ�2����֪����BDEΪֱ�������Σ���EDK���BDO��Ϊ����ֱ�������Σ�
��DE= ![]() EK=
EK= ![]() m��BD=
m��BD= ![]() OB=3
OB=3 ![]() m��
m��
��Rt��BDE��Rt��BOC��OC=m��OB=3m��DE= ![]() m��BD=3
m��BD=3 ![]() m��
m��
�� ![]() ����Rt��BDE��Rt��BOC��
����Rt��BDE��Rt��BOC��
���OBC=��DBE��
���DBC����DBE=����OBD+��OBC������DBE=��OBD=45�㣮
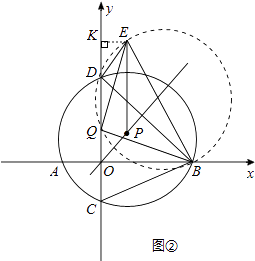
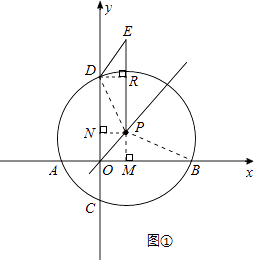
����������1����ͼ����ʾ������P��PM��x���ڵ�M������ֱ�������Σ����ô��������빴�ɶ��������B�����ꣻͬ������õ�D�����꣬����D��DR��PE�ڵ�R�����EDRΪ����ֱ�������Σ��Ӷ������E�����ꣻ��2����ͼ����ʾ�������Ƴ���BDEΪֱ�������Σ���Բ�ܽǶ�����֪��BEΪ��BDE���Բ��ֱ������ˡ�BQE=90�㣻Ȼ��֤��Rt��EQK��Rt��QBO��ͨ�������߶�֮��ı�����ϵ�����Եõ�������������ȫ�ȣ�����BQ=EQ����3����ͼ����ʾ������Ҫ����֤��Rt��BDE��Rt��BOC���õ���OBC=��DBE����������ɵá�DBC����DBE=45�㣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪б��AB��60�ף��½ǣ�����BAC��Ϊ30�㣬BC��AC���ּƻ���б���е�D����ȥ�������壨����Ӱ��ʾ����һ��ƽ����ˮƽ��CA��ƽ̨DE��һ���µ�б��BE�����뽫����2С��Ľ������ȷ��0.1�ף��ο����ݣ� ![]() ��1.732����
��1.732����
��1��������б��BE���½ǣ�����BEF��������45�㣬��ƽ̨DE�ij����Ϊ�ף�
��2��һ��������GH�����½�A��27��Զ����AG=27�ף���С����D���ý����ﶥ��H�����ǣ�����HDM��Ϊ30�㣮��B��C��A��G��H��ͬһ��ƽ���ڣ���C��A��G��ͬһ��ֱ���ϣ���HG��CG���ʽ�����GH��Ϊ�����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������5��Сľ�������ȷֱ�Ϊ��2��3��4��5��7����λ��cm������������ȡ��3����
��1���г���ѡ��3��Сľ�������п��������
��2���������3��Сľ����β˳����ӣ��������ܴ�������εĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�������һ������,��������ɣ�
(1)��֪����x��һԪһ�η���![]() ,�뻭������,���������ϱ�עa��
,�뻭������,���������ϱ�עa��![]() ��Ӧ�ĵ�,�ֱ����A,B;
��Ӧ�ĵ�,�ֱ����A,B;
(2)�ڵ�1�ʵ�������,������������һ��C��Ӧ����Ϊy,C��A�ľ�����C��B�ľ����5��,��C�ڱ�ʾ5�ĵ�����,��y��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AD��BC���Խ���AC���е�ΪO������O��AC�Ĵ��߷ֱ���AD��BC�ཻ�ڵ�E��F������AF����֤��AE=AF�� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��ѧ��2100�ˣ��ڡ����������С���У������ˡ����ɡ����ǡ��������ж�������������У���γ̣��涨ÿλѧ��������ֻ��ѡһ�ţ�Ϊ�˽�ѧ���ı�������ѧУ���������100��ѧ�������Ƴ�ͳ�Ʊ���У���γ�����ͳ�Ʊ�
�γ����� | Ƶ�� | Ƶ�ʣ�%�� |
���� | s | 0.08 |
���� | a | 0.20 |
���� | 27 | 0.27 |
�ж� | b | m |
���� | 15 | 0.15 |
�ϼ� | 100 | 1.00 |
�����ͳ�Ʊ�����Ϣ������������⣻
��1������ε����У�ѧУ��ȡ�ĵ��鷽ʽ������д���ղ顱�������顱����
��2��a= �� b= �� m=��
��3�����Ҫ����У���γ̱�����������ͳ��ͼ������ô�����ǡ���У���γ̶�Ӧ������Բ�ĽǵĶ�������
��4��������ƣ�ѡ�ж�����У���γ̵�ѧ��Լ���ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһֱ������ϵ�У�����y=mx+m��y=��mx2+2x+2��m�dz�������m��0����ͼ������ǣ� ��
A.
B.
C.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ABCD�У�AD=2AB=4��E��AD���е㣬һ���㹻������ǰ��ֱ�Ƕ������E�غϣ������ǰ��Ƶ�E��ת�����ǰ����ֱ�DZ߷ֱ�AB��BC�������ǵ��ӳ��ߣ��ڵ�M��N�����AEM=����0�㣼����90�㣩�����������ĸ����ۣ� ��AM=CN��
�ڡ�AME=��BNE��
��BN��AM=2��
��S��EMN= ![]() ��
��
������������ȷ�ĸ����ǣ� ��
A.1
B.2
C.3
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����CDΪ�ң�CD��AB�ڵ�E�������н����в��������ǣ� �� 
A.��A=��D
B.CE=DE
C.CE=BD
D.��ACB=90��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com