
【题目】如图1,已知抛物线的方程C1: ![]() (m>0)与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
(m>0)与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
(1)若抛物线C1过点M(2, 2),求实数m的值;
(2)在(1)的条件下,求△BCE的面积;
(3)在(1)的条件下,在抛物线的对称轴上找一点H,使得BH+EH最小,求出点H的坐标;
(4)在第四象限内,抛物线C1上是否存在点F,使得以点B、C、F为顶点的三角形与△BCE相似?若存在,求m的值;若不存在,请说明理由.

【答案】(1)![]() ;(2)6;(3)
;(2)6;(3) ![]() ;(4)
;(4) ![]() .
.
【解析】试题分析:(1)把M(2,2)代入函数解析式即可;(2)把![]() 代回函数解析式,求出点B、C、E的坐标即可;(3)连接CE交对称轴与点H,此时BH+EH的值最小;(4)①过点B作EC的平行线交抛物线于F,过点F作FF′⊥x轴于F′.由于∠BCE=∠FBC△BCE∽△FBC,②作∠CBF=45°交抛物线于F,过点F作FF′⊥x轴于F′,由于∠EBC=∠CBF,△BCE∽△BFC
代回函数解析式,求出点B、C、E的坐标即可;(3)连接CE交对称轴与点H,此时BH+EH的值最小;(4)①过点B作EC的平行线交抛物线于F,过点F作FF′⊥x轴于F′.由于∠BCE=∠FBC△BCE∽△FBC,②作∠CBF=45°交抛物线于F,过点F作FF′⊥x轴于F′,由于∠EBC=∠CBF,△BCE∽△BFC
试题解析:(1)将M(2, 2)代入![]() ,得
,得![]() .解得
.解得![]() .
.
(2)当![]() 时,
时, ![]() .所以C(4, 0),E(0, 2),B(-2,0).
.所以C(4, 0),E(0, 2),B(-2,0).
所以S△BCE=![]() .
.
(3)如图2,抛物线的对称轴是直线x=1,当H落在线段EC上时,BH+EH最小.
设对称轴与x轴的交点为P,那么![]() .
.
因此![]() .解得
.解得![]() .所以点H的坐标为
.所以点H的坐标为![]() .
.
(4)①如图3,过点B作EC的平行线交抛物线于F,过点F作FF′⊥x轴于F′.
由于∠BCE=∠FBC,所以当![]() ,即
,即![]() 时,△BCE∽△FBC.
时,△BCE∽△FBC.
设点F的坐标为![]() ,由
,由![]() ,得
,得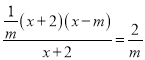 .
.
解得x=m+2.所以F′(m+2, 0).
由![]() ,得
,得![]() .所以
.所以![]() .
.
由![]() ,得
,得![]() .
.
整理,得0=16.此方程无解.
图2 图3 图4
②如图4,作∠CBF=45°交抛物线于F,过点F作FF′⊥x轴于F′,
由于∠EBC=∠CBF,所以![]() ,即
,即![]() 时,△BCE∽△BFC.
时,△BCE∽△BFC.
在Rt△BFF′中,由FF′=BF′,得![]() .
.
解得x=2m.所以F′![]() .所以BF′=2m+2,
.所以BF′=2m+2, ![]() .
.
由![]() ,得
,得![]() .解得
.解得![]() .
.
综合①、②,符合题意的m为![]() .
.


科目:初中数学 来源: 题型:
【题目】设“○”、“□”、“△”分别表示三种不同的物体,用天平比较它们质量的大小,两次情况如图所示,那么每个“○”、“□”、“△”这样的物体,按质量从小到大的顺序排列为( ) 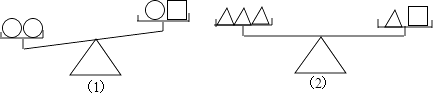
A.○□△
B.○△□
C.□○△
D.△□○
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公路上行驶的汽车急刹车时的行驶路程s(m)与时间t(s)的函数关系式为s=20t﹣5t2 , 当遇到紧急情况时,司机急刹车,但由于惯性汽车要滑行m才能停下来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抽样调查某班10名同学身高(单位:厘米)如下:160,152,165,152,160,160,170,160,165,159.则这组数据的众数是( )
A. 152B. 160C. 165D. 170
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1∶![]() ,AB=10米,AE=15米(i=1∶
,AB=10米,AE=15米(i=1∶![]() 是指坡面的铅直高度BH与水平长度AH的比).
是指坡面的铅直高度BH与水平长度AH的比).

(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将二次函数y=x2的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是( )
A.y=(x﹣1)2+2
B.y=(x+1)2+2
C.y=(x﹣1)2﹣2
D.y=(x+1)2﹣2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com