
【题目】如图,已知数轴上的点A表示的数为6,点B表示的数为﹣4,点C到点A、点B的距离相等,动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为x(x大于0)秒.
(1)点C表示的数是 ;
(2)当x= 秒时,点P到达点A处?
(3)运动过程中点P表示的数是 (用含字母x的式子表示);
(4)当P,C之间的距离为2个单位长度时,求x的值.
![]()
【答案】(1)1(2)当x=5秒时,点P到达点A处(3)2x﹣4(4)当x等于1.5或3.5秒时,P、C之间的距离为2个单位长度
【解析】
(1)根据题意得到点C是AB的中点;
(2)、(3)根据点P的运动路程和运动速度列出方程;
(4)分两种情况:点P在点C的左边有右边.
(1)依题意得,点C是AB的中点,故点C表示的数是:![]() =1.
=1.
故答案为:1;
(2)[6﹣(﹣4)]÷2=10÷2=5(秒)
答:当x=5秒时,点P到达点A处.
(3)点P表示的数是2x﹣4.
故答案是:2x﹣4;
(4)当点P在点C的左边时,2x=3,则x=1.5;
当点P在点C的右边时,2x=7,则x=3.5.
综上所述,当x等于1.5或3.5秒时,P、C之间的距离为2个单位长度.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
【题目】材料1:反射定律
当入射光线AO照射到平面镜上时,将遵循平面镜反射定律,即反射角(∠BOM)的大小等于入射角(∠AOM)的大小,显然,这两个角的余角也相等,其中法线(OM)与平面镜垂直,并且满足入射光线、反射光线(OB)与法线在同一个平面.
材料2:平行逃逸角
对于某定角∠AOB=α(0°<α<90°),点P为边OB上一点,从点P发出一光线PQ(射线),其角度为∠BPQ=β(0°<β<90°),当光线PQ接触到边OA和OB时会遵循反射定律发生反射,当光线PQ经过n次反射后与边OA或OB平行时,称角为定角α的n阶平行逃逸角,特别地,当光线PQ直接与OA平行时,称角β为定角α的零阶平行逃逸角.
(1)已知∠AOB=α=20°,
①如图1,若PQ∥OA,则∠BPQ= °,即该角为α的零阶平行逃逸角;
②如图2,经过一次反射后的光线P1Q∥OB,此时的∠BPP1为α的平行逃逸角,求∠BPP1的大小;
③若经过两次反射后的光线与OA平行,请补全图形,并直接写出α的二阶平行逃逸角为 °;
(2)根据(1)的结论,归纳猜想对于任意角α(0°<α<90°),其n(n为自然数)阶平行逃逸角β= (用含n和a的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校“数学魔盗团”社团准备购买A,B两种魔方,已知购买2个A种魔方和6个B种魔方共需130元,购买1个A种魔方比1个B种魔方多花5元.

(1)求这两种魔方的单价;
(2)结合社员们的需求,社团决定购买A,B两种魔方共100个(其中A种魔方不超过50个).“双11期间”某商店有两种优惠活动,如图所示.请根据以上信息填空:购买A种魔方________个时选择活动一盒活动二购买所需费用相同.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年12月至1月期间由于空气污染严重,天空中被浓浓的雾霾笼罩着,大多数中小学校为了学生的健康,都不得不停课.针对这一情况有关部门对停课在家的学生家长进行了抽样调查.现将学生家长对这一事件态度的调查结果分为四个等级:“A﹣﹣非常不同意”、“B﹣﹣比校同意”、“C﹣﹣不太同意”、“D﹣﹣非常同意”,并将统计结果绘制成如下两幅不完整的统计图. 请根据以上信息,解答下列问题:
(1)补全上面的条形统计图和扇形统计图;
(2)所抽样调查学生家长的人数为人;
(3)若所调查学生家长的人数为1600人,非常不同意停课的人数为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
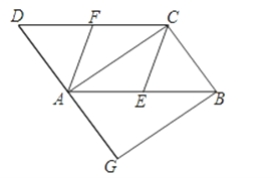
【题目】如图,在ABCD中,E、F分别为边AB、CD的中点,AC是对角线,过点B作BG∥AC交DA的延长线于点G.
(1)求证:CE∥AF;
(2)若∠G=90°,求证:四边形CEAF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在求1+3+32+33+34+35+36+37+38的值时,张红发现:从第二个加数起每一个加数都是前一个加数的3倍,于是她假设:S=1+3+32+33+34+35+36+37+38①, 然后在①式的两边都乘以3,得:3S=3+32+33+34+35+36+37+38+39②,
②﹣①得,3S﹣S=39﹣1,即2S=39﹣1,
所以S= ![]() .
.
得出答案后,爱动脑筋的张红想:如果把“3”换成字母m(m≠0且m≠1),能否求出1+m+m2+m3+m4+…+m2016的值?如能求出,其正确答案是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC与BD相交于点O,∠D=∠C,添加下列哪个条件后,仍不能使△ADO≌△BCO的是( )

A. AD=BC B. AC=BD C. OD=OC D. ∠ABD=∠BAC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com