
 如图,大半圆O与小半圆O1相切于点C,大半圆的弦AB与小半圆相切于F,且AB∥CD,AB=4cm,求阴影部分的面积.
如图,大半圆O与小半圆O1相切于点C,大半圆的弦AB与小半圆相切于F,且AB∥CD,AB=4cm,求阴影部分的面积. 分析 首先连接OA,O1F,过点O作OE⊥AB于点E,由垂径定理即可求得AE=BE,又由大半圆的弦AB与小半圆相切于F,且AB∥CD,可得O1F=OE,继而可得S阴影=S大半圆-S小半圆=$\frac{1}{2}$π(OA2-EO2).
解答 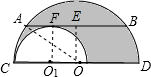 解:连接OA,O1F,过点O作OE⊥AB于点E,
解:连接OA,O1F,过点O作OE⊥AB于点E,
∴AE=BE=$\frac{1}{2}$AB=$\frac{1}{2}$×4=2(cm),
∵大半圆的弦AB与小半圆相切于F,
∴O1F⊥AB,
∵AB∥CD,
∴O1F=OE,
由勾股定理知,OA2-EO2=AE2=4,
∴S阴影=S大半圆-S小半圆=$\frac{1}{2}$π(OA2-EO2)=2π(cm2).
点评 此题考查了切线的性质以及垂径定理.注意准确作出辅助线是解此题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
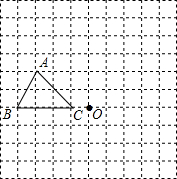 在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上.
在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
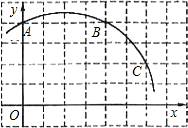 如图,直角坐标系中一条圆弧经过正方形网格的格点A(0,4)、B(4,4)、C(6,2).
如图,直角坐标系中一条圆弧经过正方形网格的格点A(0,4)、B(4,4)、C(6,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 收入x (单位:元) | 600≤x <1000 | 1000≤x <1400 | 1400≤x <1800 |
| 人数 | 12 | 50 | 18 |
| 收入x (单位:元) | 1000≤x <1400 | 1400≤x <1800 | 1800≤x <2200 |
| 人数 | 12 | 50 | 18 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com