
分析 根据所给的已知条件,找出题目中的变化规律,得出当n分别为奇数和偶数时的坐标,即可解决问题.
解答 解:(1)根据题意得:
P1(1,-1)=(0,2),
P2(1,-1)=P1[P1(1,-1)]=P1(0,2)=(2,-2)
P3(1,-1)=P1[P2(1,-1)]=P1(2,-2)=(0,4),
P4(1,-1)=P1[P3(1,-1)]=P1(0,4)=(4,-4)
故答案为:0,2;0,2;2,-2;2,-2;0,4;0,4;4,-4;
(2)根据(1)的规律可知;
P5(1,-1)=P1[P4(1,-1)]=P1(4,-4)=(0,8),
P6(1,-1)=P1[P5(1,-1)]=P1(0,8)=(8,-8),
…
当n为奇数时,Pn(1,-1)=)=(0,${2}^{\frac{n+1}{2}}$),
当n为偶数时,Pn(1,-1)=(${2}^{\frac{n}{2}}$,-${2}^{\frac{n}{2}}$),
∴P2013(1,-1)=(0,21007).
点评 本题考查了点的坐标,解题的关键是找出数字的变化,得出当n为偶数时的规律,并应用此规律解题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
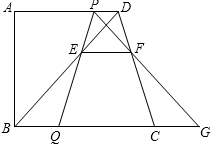 如图,已知在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=11,BC=13,AB=12.动点P、Q分别在边AD和BC上,且BQ=3DP.线段PQ与BD相交于点E,过点E作EF∥BC,交CD于点F,射线PF交BC的延长线于点G,设DP=x.
如图,已知在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=11,BC=13,AB=12.动点P、Q分别在边AD和BC上,且BQ=3DP.线段PQ与BD相交于点E,过点E作EF∥BC,交CD于点F,射线PF交BC的延长线于点G,设DP=x.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
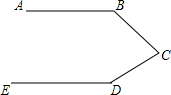 如图,某工件要求AB∥ED,质检员小李量得∠ABC=146°,∠BCD=60°,∠EDC=154°,则此工件合格.(填“合格”或“不合格”)
如图,某工件要求AB∥ED,质检员小李量得∠ABC=146°,∠BCD=60°,∠EDC=154°,则此工件合格.(填“合格”或“不合格”)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com