
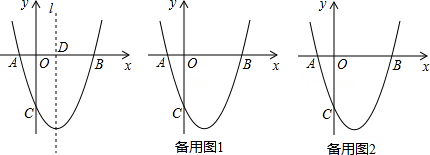
分析 (1)直接利用交点式将点A(-1,0),B(3,0),代入求出即可;
(2)利用切线的性质得出DP垂直平分AB,即DP是△ABP斜边中线,进而得出P点坐标;
(3)利用当MA⊥AC以及MC⊥AC进而利用相似三角形的判定与性质求出即可.
解答 解:(1)由题意得:y=(x+1)(x-3),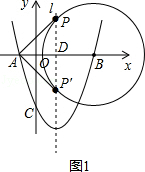
即y=x2-2x-3;
(2)如图1,
∵直线AP与⊙B相切,
∴AP⊥BP,
∵DP垂直平分AB,即DP是△ABP斜边中线,
∴DP=$\frac{1}{2}$AB=2,
∴P(1,2)或(1,-2)
(3)两种情况,设M(m,m2-2m-3),
如图2,过A作AM⊥AC交抛物线于点M,作MN⊥x轴于点N,
∴∠MAN+∠CAO=90°,∠MAN+∠AMN=90°,
∴∠CAO=∠AMN,
∵∠AOC=∠MNA=90°,
∴△AOC∽△MNA,
∴$\frac{AO}{CO}$=$\frac{MN}{AN}$,即$\frac{1}{3}$=$\frac{{m}^{2}-2m-3}{m+1}$,
解得:m1=-1(舍),m2=$\frac{10}{3}$,
∴M($\frac{10}{3}$,$\frac{13}{9}$),
如图3,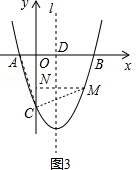
过点C作CM⊥AC交抛物线于点M,作MN⊥y轴于点N,
∴∠ACO+∠OAC=90°,∠ACO+∠NCM=90°,
∴∠OAC=∠NCM,
又∵∠AOC=∠CNM=90°,
∴△AOC∽△CNM,
∴$\frac{AO}{CO}$=$\frac{NC}{MN}$,即,$\frac{1}{3}$=$\frac{3-(-{m}^{2}+2m+3)}{m}$,
解得m1=0,m2=$\frac{7}{3}$,
∴M($\frac{7}{3}$,-$\frac{20}{9}$),
综上,在抛物线上存在点M($\frac{10}{3}$,$\frac{13}{9}$)或($\frac{7}{3}$,-$\frac{20}{9}$),使得△ACM是以AC为直角边的直角三角形.
点评 此题主要考查了二次函数综合以及相似三角形的判定与性质、切线的性质以及直角三角形的性质等知识,正确分类讨论得出是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
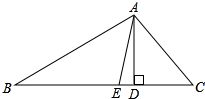 已知,如图在△ABC中,AD,AE分别是△ABC的高和角平分线,
已知,如图在△ABC中,AD,AE分别是△ABC的高和角平分线,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
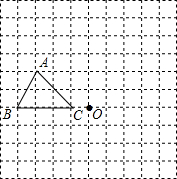 在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上.
在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
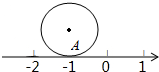 如图,圆的直径为1个单位长度,该圆上的点A与数轴上表示-1的点重合,将圆沿数轴滚动1周,点A到达点A′的位置,则点A′表示的数是( )
如图,圆的直径为1个单位长度,该圆上的点A与数轴上表示-1的点重合,将圆沿数轴滚动1周,点A到达点A′的位置,则点A′表示的数是( )| A. | π-1 | B. | -π-1 | C. | -π-1或π-1 | D. | -π-1或π﹢1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com