
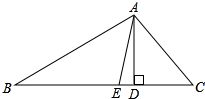
 已知,如图在△ABC中,AD,AE分别是△ABC的高和角平分线,
已知,如图在△ABC中,AD,AE分别是△ABC的高和角平分线,分析 (1)在三角形ABC中,由∠B与∠C的度数求出∠BAC的度数,根据AE为角平分线求出∠BAE的度数,由∠BAD-∠B即可求出∠DAE的度数;
(2)仿照(1)得出∠DAE与α,β的关系即可.
解答 解:(1)∵∠B=30°,∠C=50°,
∴∠BAC=180°-∠B-∠C=100°,
又∵AE是△ABC的角平分线,
∴∠BAE=$\frac{1}{2}$∠BAC=50°,
∵AD是△ABC的高,
∴∠BAD=90°-∠B=90°-30°=60°,
则∠DAE=∠BAD-∠BAE=10°;
(2)由(1)得:∠DAE=$\frac{1}{2}$(β-α).
点评 此题考查了三角形内角和定理,以及三角形的外角性质,熟练掌握内角和定理是解本题的关键.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:解答题
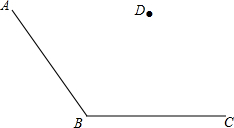 读句画图并填空:如图,点D是∠ABC内一点,根据下列语句画图.
读句画图并填空:如图,点D是∠ABC内一点,根据下列语句画图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
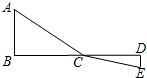 如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=5,DE=1,BD=8,设CD=x.
如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=5,DE=1,BD=8,设CD=x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
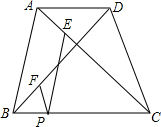 如图,梯形ABCD中,AD∥BC AB=DC=3,P是BC上一点,PE∥AB交AC于E,PF∥CD交BD于F,若PE、PF的长分别为m、n,设x=m+n,当点P在BC上移动时,x的值是否变化?若变化,求出x的取值范围.若不变,求出x的值.
如图,梯形ABCD中,AD∥BC AB=DC=3,P是BC上一点,PE∥AB交AC于E,PF∥CD交BD于F,若PE、PF的长分别为m、n,设x=m+n,当点P在BC上移动时,x的值是否变化?若变化,求出x的取值范围.若不变,求出x的值.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
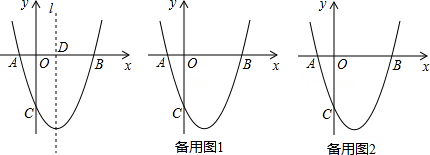
 在平面直角坐标系xOy中,直线y=kx(k为常数)与抛物线y=$\frac{1}{3}$x2-2交于A,B两点,且A点在y轴左侧,P点坐标为(0,-4),连接PA,PB.有以下说法:
在平面直角坐标系xOy中,直线y=kx(k为常数)与抛物线y=$\frac{1}{3}$x2-2交于A,B两点,且A点在y轴左侧,P点坐标为(0,-4),连接PA,PB.有以下说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
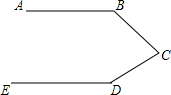 如图,某工件要求AB∥ED,质检员小李量得∠ABC=146°,∠BCD=60°,∠EDC=154°,则此工件合格.(填“合格”或“不合格”)
如图,某工件要求AB∥ED,质检员小李量得∠ABC=146°,∠BCD=60°,∠EDC=154°,则此工件合格.(填“合格”或“不合格”)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com