
 在平面直角坐标系xOy中,直线y=kx(k为常数)与抛物线y=$\frac{1}{3}$x2-2交于A,B两点,且A点在y轴左侧,P点坐标为(0,-4),连接PA,PB.有以下说法:
在平面直角坐标系xOy中,直线y=kx(k为常数)与抛物线y=$\frac{1}{3}$x2-2交于A,B两点,且A点在y轴左侧,P点坐标为(0,-4),连接PA,PB.有以下说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 (1)说法①错误.如答图1,设点A关于y轴的对称点为A′,若结论①成立,则可以证明△POA′∽△PBO,得到∠AOP=∠PBO.而∠AOP是△PBO的外角,∠AOP>∠PBO,由此产生矛盾,故说法①错误;
(2)说法②错误.如答图2,可求得(PA+AO)(PB-BO)=16为定值,故错误;
(3)说法③正确.联立方程组,求得点A、B坐标,进而求得BP、BO、BA,验证等式BP2=BO•BA成立,故正确;
(4)说法④正确.由根与系数关系得到:S△PAB=2$\sqrt{9{k}^{2}+24}$,当k=0时,取得最小值为4$\sqrt{6}$,故正确.
解答 解:设A(m,km),B(n,kn),其中m<0,n>0.
联立y=$\frac{1}{3}$x2-2与y=kx得:$\frac{1}{3}$x2-2=kx,即x2-3kx-6=0,
∴m+n=3k,mn=-6.
设直线PA的解析式为y=ax+b,将P(0,-4),A(m,km)代入得:
$\left\{\begin{array}{l}{b=-4}\\{ma+b=km}\end{array}\right.$,
解得a=$\frac{km+4}{m}$,b=-4,
∴y=($\frac{km+4}{m}$)x-4.
令y=0,得x=$\frac{4m}{km+4}$,
∴直线PA与x轴的交点坐标为($\frac{4m}{km+4}$,0).
同理可得,直线PB的解析式为y=($\frac{kn+4}{n}$)x-4,直线PB与x轴交点坐标为($\frac{4n}{kn+4}$,0).
∵$\frac{4m}{km+4}$+$\frac{4n}{kn+4}$=$\frac{8kmn+16(n+n)}{(km+4)(kn+4)}$=$\frac{8k×(-6)+16×3k}{(km+4)(kn+4)}$=0,
∴直线PA、PB与x轴的交点关于y轴对称,即直线PA、PB关于y轴对称.
(1)说法①错误.理由如下:
如答图1所示,∵PA、PB关于y轴对称,
∴点A关于y轴的对称点A′落在PB上.
连接OA′,则OA=OA′,∠POA=∠POA′.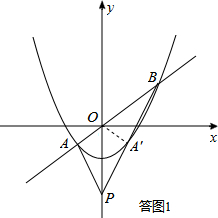
假设结论:PO2=PA•PB成立,即PO2=PA′•PB,
∴$\frac{PO}{PA′}$=$\frac{PB}{PO}$,
又∵∠BPO=∠BPO,
∴△POA′∽△PBO,
∴∠POA′=∠PBO,
∴∠AOP=∠PBO.
而∠AOP是△PBO的外角,
∴∠AOP>∠PBO,矛盾,
∴说法①错误.
(2)说法②错误.理由如下:
易知:$\frac{OB}{OA}$=-$\frac{n}{m}$,
∴OB=-$\frac{n}{m}$OA.
由对称可知,PO为△APB的角平分线,
∴$\frac{PB}{PA}$=$\frac{OB}{OA}$,
∴PB=-$\frac{n}{m}$PA.
∴(PA+AO)(PB-BO)=(PA+AO)[-$\frac{n}{m}$PA-(-$\frac{n}{m}$OA)]=-$\frac{n}{m}$(PA+AO)(PA-OA)=-$\frac{n}{m}$(PA2-AO2).
如答图2所示,过点A作AD⊥y轴于点D,则OD=-km,PD=4+km.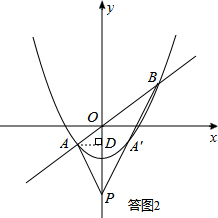
∴PA2-AO2=(PD2+AD2)-(OD2+AD2)=PD2-OD2=(4+km)2-(-km)2=8km+16,
∵m+n=3k,∴k=$\frac{1}{3}$(m+n),
∴PA2-AO2=8•$\frac{1}{3}$(m+n)•m+16=$\frac{8}{3}$m2+$\frac{8}{3}$mn+16=$\frac{8}{3}$m2+$\frac{8}{3}$×(-6)+16=$\frac{8}{3}$m2.
∴(PA+AO)(PB-BO)=-$\frac{n}{m}$(PA2-AO2)=-$\frac{n}{m}$•$\frac{8}{3}$m2=-$\frac{8}{3}$mn=-$\frac{8}{3}$×(-6)=16.
即:(PA+AO)(PB-BO)为定值,所以说法②错误.
(3)说法③正确.理由如下:
当k=-$\frac{\sqrt{3}}{3}$时,联立方程组:$\left\{\begin{array}{l}{y=-\frac{\sqrt{3}}{3}x}\\{y=\frac{1}{3}{x}^{2}-2}\end{array}\right.$,得A(-2$\sqrt{3}$,2),B($\sqrt{3}$,-1),
∴BP2=12,BO•BA=2×6=12,
∴BP2=BO•BA,故说法③正确.
(4)说法④正确.理由如下:
S△PAB=S△PAO+S△PBO=$\frac{1}{2}$OP•(-m)+$\frac{1}{2}$OP•n=$\frac{1}{2}$OP•(n-m)=2(n-m)=2$\sqrt{(m+n)^{2}-4mn}$=2$\sqrt{9{k}^{2}+24}$,
∴当k=0时,△PAB面积有最小值,最小值为2$\sqrt{24}$=4$\sqrt{6}$.
故说法④正确.
综上所述,正确的说法是:③④.
故选B
点评 本题是代数几何综合题,难度很大.解答中首先得到两个基本结论,其中PA、PB的对称性是判定说法①的基本依据,根与系数关系的结论是判定说法②、④的关键依据.正确解决本题的关键是打好数学基础,将平时所学知识融会贯通、灵活运用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
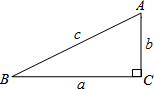 如图,在Rt△ABC中,∠C=90°,a、b、c分别表示∠A、∠B、∠C的对边.
如图,在Rt△ABC中,∠C=90°,a、b、c分别表示∠A、∠B、∠C的对边.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
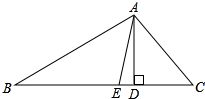 已知,如图在△ABC中,AD,AE分别是△ABC的高和角平分线,
已知,如图在△ABC中,AD,AE分别是△ABC的高和角平分线,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
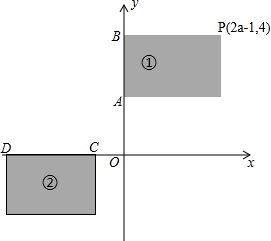 如图,在平面直角坐标系中,A(0,2),B(0,4),
如图,在平面直角坐标系中,A(0,2),B(0,4),查看答案和解析>>
科目:初中数学 来源: 题型:选择题
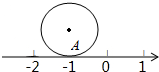 如图,圆的直径为1个单位长度,该圆上的点A与数轴上表示-1的点重合,将圆沿数轴滚动1周,点A到达点A′的位置,则点A′表示的数是( )
如图,圆的直径为1个单位长度,该圆上的点A与数轴上表示-1的点重合,将圆沿数轴滚动1周,点A到达点A′的位置,则点A′表示的数是( )| A. | π-1 | B. | -π-1 | C. | -π-1或π-1 | D. | -π-1或π﹢1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com