
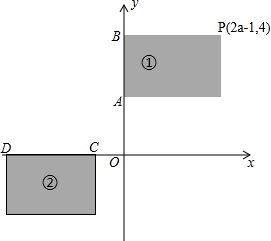
 如图,在平面直角坐标系中,A(0,2),B(0,4),
如图,在平面直角坐标系中,A(0,2),B(0,4),分析 (1)根据第一象限和第三象限点的坐标特征得到2a-1>0,且4-3a<0,然后求出两不等式的公共部分即可;
(2)利用坐标表示线段长,然后根据矩形面积公式求解;
(3)先计算出S①-S②=11-5a,然后分类讨论:当11-5a>0,即$\frac{4}{3}$<a<$\frac{11}{5}$时,S①-S②>0;当11-5a=0,a=$\frac{11}{5}$时,S①=S②;当11-5a<0,a>$\frac{11}{5}$时,S①-S②<0.
解答 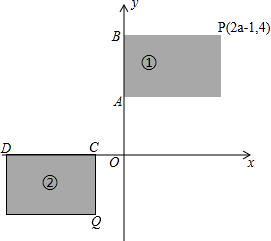 解:(1)2a-1>0,且4-3a<0,解得a>$\frac{4}{3}$;
解:(1)2a-1>0,且4-3a<0,解得a>$\frac{4}{3}$;
(2)①AB=4-2=2,PB=2a-1,则S①=2(2a-1)=4a-1;
CD=-1-(-4)=3,CQ=3a-4,则S②=3(3a-4)=9a-12;
故答案为4a-1,9a-12;
(3)S①-S②=4a-1-(9a-12)=11-5a,
当11-5a>0,$\frac{4}{3}$<a<$\frac{11}{5}$时,S①-S②>0,则选择以A,B,P为顶点构造如图①所示的长方形;
当11-5a=0,a=$\frac{11}{5}$时,S①=S②,则选择两个都一样;
当11-5a<0,a>$\frac{11}{5}$时,S①-S②<0,则选择以C,D,Q为顶点构造如图②所示的长方形.
点评 本题考查了坐标与图形性质:利用点的坐标计算相应线段的长和判断线段与坐标轴的位置关系;记住各象限内点的坐标特征.也考查了矩形面积公式.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 在平面直角坐标系xOy中,直线y=kx(k为常数)与抛物线y=$\frac{1}{3}$x2-2交于A,B两点,且A点在y轴左侧,P点坐标为(0,-4),连接PA,PB.有以下说法:
在平面直角坐标系xOy中,直线y=kx(k为常数)与抛物线y=$\frac{1}{3}$x2-2交于A,B两点,且A点在y轴左侧,P点坐标为(0,-4),连接PA,PB.有以下说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,O为坐标原点,点A坐标为(1,0),以OA为边在第一象限内作等边△OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.
在平面直角坐标系中,O为坐标原点,点A坐标为(1,0),以OA为边在第一象限内作等边△OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com