
 在平面直角坐标系中,O为坐标原点,点A坐标为(1,0),以OA为边在第一象限内作等边△OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.
在平面直角坐标系中,O为坐标原点,点A坐标为(1,0),以OA为边在第一象限内作等边△OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.分析 (1)根据等边三角形的性质,可得∠OBA与∠DBC的关系,根据等式的性质,可得∠OBC=∠ABD,根据“SAS”得到△OBC≌△ABD,即可得到对应边AD与OC相等,由OC表示出AD即可;
(2)根据全等三角形的性质,可得∠BAD=∠BOC=60°,根据等边三角形的性质,可得∠BAO=60°,根据平角定义及对顶角相等,可得∠OAE=60°,根据tan60°的定义求出OE的长,确定出点E的坐标,根据待定系数法,将点A和E的坐标代入即可确定出解析式;
(3)①根据平行线的性质,可得EF与EA重合,根据三角形的中位线,可得A为OC中点,根据线段中点的性质,可得C的坐标;根据等边三角形的性质,可得DF⊥BC,根据平行线的性质,可得BF与OB垂直,根据切线的判定,可得答案;
②根据等边三角形的“三线合一”,可得DF垂直平分BC,根据轴对称的性呢,可得GB为HC+HG的最小值,根据圆的性质,可得FB,FC及FG相等,根据直角三角形的判定,可得△BCG为直角三角形;根据“三线合一”,可得∠CBG为30°,根据锐角三角函数,可得BG,根据等边三角形的性质,可得BM及AM,根据勾股定理表示出BC的长即可.
解答 解:(1)∵△OAB和△BCD都为等边三角形,
∴OB=AB,BC=BD,∠OBA=∠DBC=60°,即∠OBA+∠ABC=∠DBC+∠ABC,
∴∠OBC=∠ABD,
在△OBC和△ABD中,
$\left\{\begin{array}{l}{OB=OA}\\{∠OBC=∠ABD}\\{BC=BD}\end{array}\right.$,
∴△OBC≌△ABD(SAS),
∴AD=OC=1+x;
(2)随着C点的变化,直线AE的位置不变.理由如下:
由△OBC≌△ABD,得到∠BAD=∠BOC=60°,
又∵∠BAO=60°,
∴∠DAC=60°,
∴∠OAE=60°,又OA=1,
在直角三角形AOE中,tan60°=$\frac{DE}{OA}$,则OE=$\sqrt{3}$,
点E坐标为(0,-$\sqrt{3}$),A(1,0),
设直线AE解析式为y=kx+b,把E和A的坐标代入,得
$\left\{\begin{array}{l}{k+b=0}\\{b=-\sqrt{3}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=\sqrt{3}}\\{b=-\sqrt{3}}\end{array}\right.$,
所以直线AE的解析式为y=$\sqrt{3}$x-$\sqrt{3}$;
(3)①根据题意画出图形,如图所示1: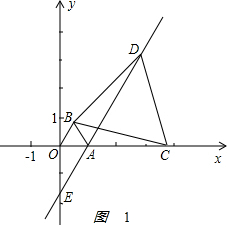
∵∠BOA=∠DAC=60°,EA∥OB,又EF∥OB,则EF与EA所在的直线重合,
∴点F为DE与BC的交点,
又F为BC中点,
∴A为OC中点,又AO=1,则OC=2,
∴当C的坐标为(2,0)时,EF∥OB;
这时直线BO与⊙F相切,理由如下:
∵△BCD为等边三角形,F为BC中点,
∴DF⊥BC,又EF∥OB,
∴FB⊥OB,即∠FBO=90°,
故直线BO与⊙F相切;
②根据题意画出图形,如图所示: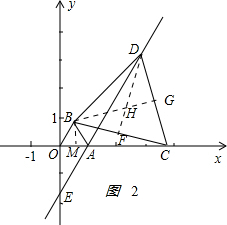 ,
,
由点B,点C及点G在圆F的圆周上得:FB=FC=FG,即FG=$\frac{1}{2}$BC,
∴△CBG为直角三角形,又△BCD为等边三角形,
∴BG为∠CBD的平分线,即∠CBG=30°,
过点B作x轴的垂直,交x轴于点M,由△OAB为等边三角形,
∴M为OA中点,即MA=$\frac{1}{2}$,BM=3$\sqrt{2}$,MC=AC+AM=x+$\frac{1}{2}$.
在直角三角形BCM中,根据勾股定理得:
BC=$\sqrt{B{M}^{2}+M{C}^{2}}$=$\sqrt{{x}^{2}+x+1}$,
∵DF垂直平分BC,
∴B和C关于DF对称,
∴HC=HB,
则HC+HG=BG,此时BG最小,
在直角三角形BCG中,
BG=BCcos30°=$\frac{1}{2}$$\sqrt{3{x}^{2}+3x+3}$.
点评 本题考查了一次函数综合题,(1)利用了等边三角形的性质,全等三角形的判定与性质;(2)利用了全等三角形的性质,等边三角形的性质,待定系数法求函数解析式;(3)①利用了直线与圆的位置关系;②利用了轴对称-最短路线问题.


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,A(0,2),B(0,4),
如图,在平面直角坐标系中,A(0,2),B(0,4),查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
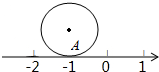 如图,圆的直径为1个单位长度,该圆上的点A与数轴上表示-1的点重合,将圆沿数轴滚动1周,点A到达点A′的位置,则点A′表示的数是( )
如图,圆的直径为1个单位长度,该圆上的点A与数轴上表示-1的点重合,将圆沿数轴滚动1周,点A到达点A′的位置,则点A′表示的数是( )| A. | π-1 | B. | -π-1 | C. | -π-1或π-1 | D. | -π-1或π﹢1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
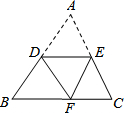 将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,下列结论中,一定正确的个数是( )
将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,下列结论中,一定正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com