
分析 (1)因为直线m:y=kx+b与直线n:y=2x平行,所以k值相等,即k=2,又因该直线过点(1,1),所以就有1=2×1+b,从而可求出b的值.
(2)根据求得的直线m的解析式,令y=0,求得与x轴的交点坐标,令x=0,求得与y轴的交点坐标;
(3)求得直线y=-3x-1与坐标轴的交点,然后根据三角形面积公式求得即可.
解答 解:(1)∵直线m:y=kx+b与直线n:y=2x平行,
∴k=2,
则直线m即为y=2x+b.
∵直线l过点(1,1),
∴1=2×1+b,
∴b=-1.
∴直线m的解析式为y=2x-1.
(2)当y=0时,解得x=$\frac{1}{2}$,
当x=0时,解得y=-1,
∴直线m与两坐标轴的交点坐标是($\frac{1}{2}$,0),(0,-1);
(3)∵直线y=-3x-1与两坐标轴的交点坐标是(-$\frac{1}{3}$,0),(0,-1),
∴直线m与直线y=-3x-1以及x轴围成的三角形面积=$\frac{1}{2}$×($\frac{1}{2}$+$\frac{1}{3}$)×1=$\frac{5}{12}$.
点评 本题考查了两条直线平行或相交问题,一次函数上点的坐标特征以及三角形的面积等,难度不大,关键求出未知方程的解析式.


科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,O为坐标原点,点A坐标为(1,0),以OA为边在第一象限内作等边△OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.
在平面直角坐标系中,O为坐标原点,点A坐标为(1,0),以OA为边在第一象限内作等边△OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
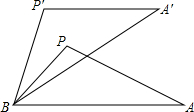 如图,△APB绕点B按逆时针方向旋转30°后,得到△A′P′B,且AB=4,那么AA′的长为2$\sqrt{6}$-2$\sqrt{2}$.(不取近似值,sin15°=$\frac{\sqrt{6}-\sqrt{2}}{4}$,cos15°=$\frac{\sqrt{6}+\sqrt{2}}{4}$)
如图,△APB绕点B按逆时针方向旋转30°后,得到△A′P′B,且AB=4,那么AA′的长为2$\sqrt{6}$-2$\sqrt{2}$.(不取近似值,sin15°=$\frac{\sqrt{6}-\sqrt{2}}{4}$,cos15°=$\frac{\sqrt{6}+\sqrt{2}}{4}$)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com