练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．解方程：（3x-2）2=（2x-3）2．

    分析 利用直接开平方法得到3x-2=±（2x-3），然后解两个一次方程即可．

    解答 解：3x-2=±（2x-3），
    3x-2=2x-3或3x-2=-2x+3，
    所以x1=-1，x2=1．

    点评 本题考查了解一元二次方程-直接开平方法：形如x2=p或（nx+m）2=p（p≥0）的一元二次方程可采用直接开平方的方法解一元二次方程．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    5．如图，已知正方形ABCD的边长为3，如果将线段AC绕点A旋转后，点C落在BA延长线上的C′点处，那么tan∠ADC′=$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图，在Rt△ABC中，AB=AC=2$\sqrt{2}$．∠BAC=90°，以A为圆心1为半径作圆，O为BC上的一动点，以O为圆心OB为半径作圆．若⊙0与⊙A相切，求0B的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

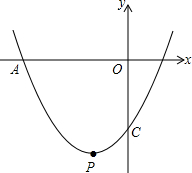    5．已知平面直角坐标系xOy，抛物线y=$\frac{1}{2}$x2+bx+c经过点A（-3，0）、C（0，-$\frac{3}{2}$）．
    （1）求该抛物线顶点P的坐标；
    （2）过C作AC的垂线，求此垂线的函数关系式；
    （3）在抛物线求点Q，使∠QAC=∠PAC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

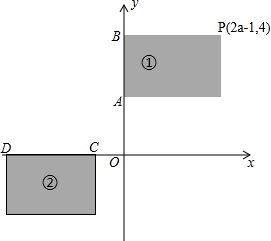    12．如图，在平面直角坐标系中，A（0，2），B（0，4），
    C（-1，0），D（-4，0），点P（2a-1，4）是第一象限
    内一点，点Q（-1，4-3a）是第三象限内一点
    （1）求a的取值范围；
    （2）①以A，B，P为顶点构造如图①所示的长方形，面积记为
    S①；以C，D，Q为顶点构造如图②所示的长方形，面积记为
    S②，则S①=4a-1；S②=9a-12（用含a的式子表示）；
    ②若想在构造的两个长方形中选择一个面积较大的，你认为应该如何选？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．已知关于x的方程x2+（2k+1）x+k2=0的两个实数根的平方和是7，则k=-3或1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．九（1）班数学课题学习小组，为了研究学习二次函数问题，他们经历了实践--应用--探究的过程：
    （1）实践：他们对一条公路上横截面的单向双车道的隧道（如图①）进行测量，测得一隧道的路面宽为10m，隧道顶部最高处距地面6.25m，并画出了隧道截面图，建立了如图②所示的直角坐标系，请你求出抛物线的解析式．（2）应用：规定机动车辆通过隧道时，车顶部与隧道在竖直方向上的高度差至少为0.5m，为了确保安全，问该隧道能否让最宽3m，最高3.5m的两辆厢式货车居中并列行驶（两车并列行驶时不考虑两车的空隙）？
    （3）探究：该课题学习小组为进一步探抛物线的有关知识，他们借助上述抛物线模型，提出了一下两个问题，请予解答：
    Ⅰ如图③，在抛物线内作矩形ABCD，使顶点C、D落在抛物线上，顶点A、B落在x轴上设矩形ABCD的周长为l，求l的最大值．
    Ⅱ如图④，过原点作一条y=x的直线OM，交抛物线于点M，交抛物线对称轴于点N，P　为直线0M上一动点，过P点作x轴的垂线交抛物线于点Q．问在直线OM上是否存在点P，使以P、N、Q为顶点的三角形是等腰直角三角形？若存在，请求出P点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．已知，直线m：y=kx+b与直线n：y=2x平行，且过点（1，1）
    （1）求直线m的表达式；
    （2）求出直线m与两坐标轴的交点坐标；
    （3）求直线m与直线y=-3x-1以及x轴围成的三角形面积．

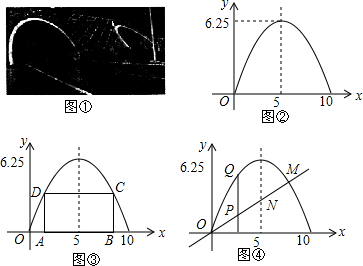
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．小明和小华在手工制作课上用铁丝制作楼梯模型，如图，那么他们两个人用的铁丝（　　）
    A．小华用的多B．小明用的多
    C．两人用的一样多D．不能确定谁用的多

    查看答案和解析>>

    同步练习册答案