
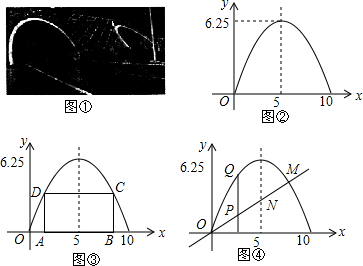
分析 (1)利用顶点式将顶点坐标(5,6.25)代入,求出二次函数解析式即可;
(2)根据已知得出当x=2时,正好是汽车宽度,代入函数解析式求出即可;
(3)I.首先用未知数表示出矩形周长,再利用二次函数最值公式求出;
II•利用等腰直角三角形的性质得出QN=AB=AO,以及P在y=x的图象上,即可得出P点的坐标.
解答 解:(1)根据坐标系可知此函数顶点坐标为(5,6.25),且图象过(10,0)点,
代入顶点式得:
y=a(x-5)2+6.25,
∴0=a(10-5)2+6.25,
解得:a=-0.25,
∴y=-0.25(x-5)2+6.25;
(2)当最宽3m,最高3.5m的两辆厢式货车居中并列行驶时,
∴10-3×2=4,
4÷2=2,
∴x=2代入解析式得:
y=-0.25(2-5)2+6.25;
y=4,
4-3.5=0.5,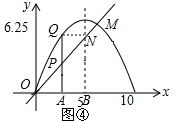
∴隧道能让最宽3m,最高3.5m的两辆厢式货车居中并列行驶;
(3)I.假设AO=x,可得AB=10-2x,
∴AD=-0.25(x-5)2+6.25;
∴矩形ABCD的周长为l为:l=2[-0.25(x-5)2+6.25]+2(10-2x)=-0.5x2+x+20,
∴l的最大值为:$\frac{4ac-{b}^{2}}{4a}$=$\frac{4×(-\frac{1}{2})×20-1}{-2}$=20.5.
II•如图④,当以P、N、Q为顶点的三角形是等腰直角三角形,
∵P在y=x的图象上,过P点作x轴的垂线交抛物线于点Q.
∴∠POA=∠OPA=45°,
∴Q点的纵坐标为5,
∴5=$\frac{-{m}^{2}+10m}{4}$,
解得:m=5±$\sqrt{5}$,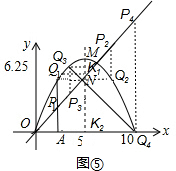
如图⑤,当∠P3NQ3=90°时,过点Q3作Q3K1⊥对称轴,
当△NQ3K1为等腰直角三角形时,△NP3Q3为等腰直角三角形,
Q点在OM的上方时,P3Q3=2Q3K1,P3Q3=-$\frac{1}{4}{x}^{2}$+$\frac{5}{2}$-x,
Q3K1=5-x,
Q点在OM的下方时,P4Q4=2Q4K2,P4Q4=x-(-$\frac{1}{4}{x}^{2}$+$\frac{5}{2}$),
Q4K2=x-5,
∴$\frac{1}{4}$x2-$\frac{7}{2}$x+10=0,
解得:x1=4,x2=10,
P3(4,4),P4(10,10)
∴使以P、N、Q为顶点的三角形是等腰直角三角形,P点的坐标为:
(5-$\sqrt{5}$,5-$\sqrt{5}$)或(5+$\sqrt{5}$,5+$\sqrt{5}$)或(4,4)或(10,10).
点评 此题主要考查了顶点式求二次函数解析式以及二次函数最值求法和等腰直角三角形的性质,根据函数图象获取正确点的坐标以及利用y=x图象上点的性质是解决问题的关键.


科目:初中数学 来源: 题型:解答题
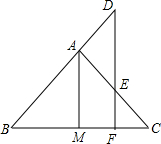 如图,在△ABC中,AB=AC,AM为△ABC底边上的中线,点D在BA的延长线上,E在AC上,且AD=AE,DE交BC于F,求证:DF⊥BC.
如图,在△ABC中,AB=AC,AM为△ABC底边上的中线,点D在BA的延长线上,E在AC上,且AD=AE,DE交BC于F,求证:DF⊥BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,O为坐标原点,点A坐标为(1,0),以OA为边在第一象限内作等边△OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.
在平面直角坐标系中,O为坐标原点,点A坐标为(1,0),以OA为边在第一象限内作等边△OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com