
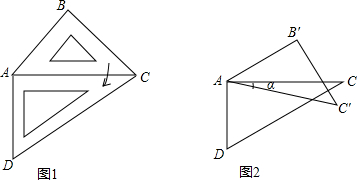
分析 (1)如图1,易得∠BCD=75°,然后在△BDC中运用三角形内角和定理就可解决问题;
(2)①如图2,当α=15°时,可得∠BAC=∠ACD=30°,从而可得AB∥CD;②当α=45°时,可求出∠CEC1,然后利用三角形的内角和定理可求出∠EOC1,然后利用三角形外角的性质可求出∠DBC1+∠BDC,就可求出∠DBC1+∠BDC+∠CAC1;③当0°<α≤45°时,在△ACC1中,利用三角形内角和定理可得∠CAC1+30°+∠OCC1+45°+∠OC1C=180°,根据三角形外角的性质可得∠DBC1+∠BDC=∠DOC=∠OCC1+∠OC1C,从而可得∠DBC1+∠CAC1+∠BDC=105°.
解答 解:(1)如图1,在△BDC中,∠BCD=45°+30°=75°,
∴∠DBC+∠BDC=180°-∠BCD=105°.
故答案为105°;
(2)①如图2,当α=15°时,∠BAC=45°-15°=30°,
∴∠BAC=∠ACD=30°,
∴AB∥CD.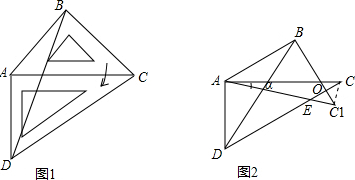
故答案为15°;
②当α=45°时,∠CEC1=∠EAC+∠ACE=45°+30°=75°,
∴∠EOC1=180°-∠CEC1-∠BC1A=180°-75°-45°=60°,
∴∠DBC1+∠BDC=∠EOC1=60°;
∴∠DBC1+∠BDC+∠CAC1=60°+45°=105°.
故答案为105°;
③当0°<α≤45°时,∠DBC1+CAC1+∠BDC的值的大小不变,等于105°.
证明:在△ACC1中,
∵∠CAC1+∠ACC1+∠AC1C=∠CAC1+∠ACO+∠OCC1+∠AC1B+∠OC1C=∠CAC1+30°+∠OCC1+45°+∠OC1C=180°,
∠DBC1+∠BDC=∠DOC1=∠OCC1+∠OC1C,
∴∠CAC1+75°+∠DBC1+∠BDC=180°,
∴∠DBC1+∠CAC1+∠BDC=105°.
点评 本题主要考查了三角形内角和定理、三角形外角的性质、平行线的判定等知识,构造8字型将∠DBC1+∠BDC转化为∠OCC1+∠OC1C,是解决最后一小题的关键.


科目:初中数学 来源: 题型:解答题
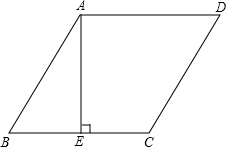 如图,在菱形ABCD中,AE⊥BC,垂足为E,EC=1,cosB=$\frac{5}{13}$.
如图,在菱形ABCD中,AE⊥BC,垂足为E,EC=1,cosB=$\frac{5}{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
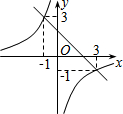 已知一次函数y1=kx+b与反比例函数y2=$\frac{k}{x}$在同一直角坐标系中的图象如图所示,则当y1>y2时,x的取值范围是( )
已知一次函数y1=kx+b与反比例函数y2=$\frac{k}{x}$在同一直角坐标系中的图象如图所示,则当y1>y2时,x的取值范围是( )| A. | x<-1或0<x<3 | B. | -1<x<0或x>3 | C. | -1<x<0 | D. | x>3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
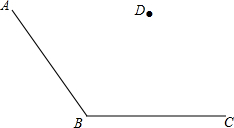 读句画图并填空:如图,点D是∠ABC内一点,根据下列语句画图.
读句画图并填空:如图,点D是∠ABC内一点,根据下列语句画图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在平面直角坐标系xOy中,直线y=kx(k为常数)与抛物线y=$\frac{1}{3}$x2-2交于A,B两点,且A点在y轴左侧,P点坐标为(0,-4),连接PA,PB.有以下说法:
在平面直角坐标系xOy中,直线y=kx(k为常数)与抛物线y=$\frac{1}{3}$x2-2交于A,B两点,且A点在y轴左侧,P点坐标为(0,-4),连接PA,PB.有以下说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com