
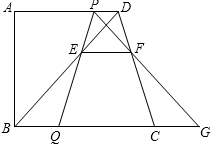
 ��ͼ����֪��ֱ������ABCD�У�AD��BC��AB��BC��AD=11��BC=13��AB=12������P��Q�ֱ��ڱ�AD��BC�ϣ���BQ=3DP���߶�PQ��BD�ཻ�ڵ�E������E��EF��BC����CD�ڵ�F������PF��BC���ӳ����ڵ�G����DP=x��
��ͼ����֪��ֱ������ABCD�У�AD��BC��AB��BC��AD=11��BC=13��AB=12������P��Q�ֱ��ڱ�AD��BC�ϣ���BQ=3DP���߶�PQ��BD�ཻ�ڵ�E������E��EF��BC����CD�ڵ�F������PF��BC���ӳ����ڵ�G����DP=x������ ��1������ƽ���ߵ����ʵá�PDE=��EBQ����EPD=��EQB����EPD�ס�EQB���������������ε����ʵ� $\frac{DP}{BQ}$=$\frac{PE}{QE}$���ɵ�$\frac{PE}{PQ}$=$\frac{1}{4}$����ΪEF��BC�����ԡ�PEF�ס�PQG������ $\frac{EF}{QG}$=$\frac{PE}{PQ}$=$\frac{1}{4}$��
��2�����ᷢ���仯����AD��BC���� $\frac{BQ}{PD}$=$\frac{CG}{PD}$���ɵ�BC=QG���ɡ�PEF�ס�PQG����S�ı���EFGQ=$\frac{15}{16}$S��PQG����á�PQG��������ɵ��ı���EFGQ�����S��
��3�����߶�PQΪ�����������PQ=PG��Ҳ������PQ=QG�����Էֿ���⼴�ɣ�
��� �⣺��1����AD��BC��
���PDE=��EBQ����EPD=��EQB��
���EPD�ס�EQB��
��$\frac{DP}{BQ}$=$\frac{PE}{QE}$��
��BQ=3DP��
��$\frac{PE}{QE}$=$\frac{1}{3}$��
��$\frac{PE}{PQ}$=$\frac{1}{4}$��
��EF��BC��
���PEF=��PQG����PFE=��G��
���PEF�ס�PQG��
��$\frac{EF}{QG}$=$\frac{PE}{PQ}$=$\frac{1}{4}$��
��2�����ᷢ���仯��
��AD��BC��
��$\frac{BQ}{PD}$=$\frac{CG}{PD}$��
��BQ=CG��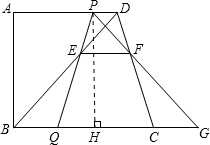
��BC=QG��
�ߡ�PEF�ס�PQG��
��S�ı���EFGQ=$\frac{15}{16}$S��PQG��
��S��PQG=$\frac{1}{2}$QG��AB=$\frac{1}{2}$BC��AB=$\frac{1}{2}$��13��12=78��
��S�ı���EFGQ=$\frac{15}{16}$��78=73.125��
��3����PH��BC��������H��
��i����PQ=PGʱ��QH=GH=$\frac{13}{2}$��
��2x+$\frac{13}{2}$=11-x��
���x=$\frac{3}{2}$��
��ii����PQ=GQʱ��PQ=$\sqrt{��11-3x��^{2}+1{2}^{2}}$=13��
���x=2��x=$\frac{16}{3}$��
��������������PQG����PQΪ���ĵ���������ʱ��x��ֵΪ$\frac{3}{2}$��2��$\frac{16}{3}$��
���� ������Ҫ���������������ε��ۺ��⣬�õ����������ε��ж������ʡ�ƽ���ߵ����ʡ���������������ؼ�����á�PEF�ס�PQG��


 ��������������������ϵ�д�
��������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
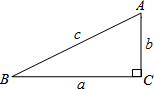 ��ͼ����Rt��ABC�У���C=90�㣬a��b��c�ֱ��ʾ��A����B����C�ĶԱߣ�
��ͼ����Rt��ABC�У���C=90�㣬a��b��c�ֱ��ʾ��A����B����C�ĶԱߣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | -3 | C�� | ��3 | D�� | 0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
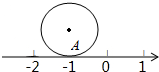 ��ͼ��Բ��ֱ��Ϊ1����λ���ȣ���Բ�ϵĵ�A�������ϱ�ʾ-1�ĵ��غϣ���Բ���������1�ܣ���A�����A���λ�ã����A���ʾ�����ǣ�������
��ͼ��Բ��ֱ��Ϊ1����λ���ȣ���Բ�ϵĵ�A�������ϱ�ʾ-1�ĵ��غϣ���Բ���������1�ܣ���A�����A���λ�ã����A���ʾ�����ǣ�������| A�� | ��-1 | B�� | -��-1 | C�� | -��-1���-1 | D�� | -��-1��Щ�1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
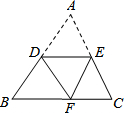 ��������ֽƬABC��DE�۵���ʹ��A����BC���ϵĵ�F������DE��BC�����н����У�һ����ȷ�ĸ����ǣ�������
��������ֽƬABC��DE�۵���ʹ��A����BC���ϵĵ�F������DE��BC�����н����У�һ����ȷ�ĸ����ǣ�������| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����һ������ȷ�� | B�� | ����ȷ���жϾͲ������� | ||
| C�� | �����ⶼ�ǹ��� | D�� | �������������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com