
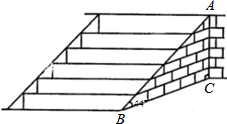
 武当山风景管理区,为提高游客到某景点的安全性,决定将到达该景点的步行台阶进行改善,把倾角由44°减至32°,已知原台阶AB的长为5米(BC所在地面为水平面).
武当山风景管理区,为提高游客到某景点的安全性,决定将到达该景点的步行台阶进行改善,把倾角由44°减至32°,已知原台阶AB的长为5米(BC所在地面为水平面).分析 (1)要求台阶加长的部分,需求台阶改善后的新长度,改后的台阶组成的直角三角形中,有坡角的度数,只要知道台阶的垂直距离便可,因为台阶修改前后高没变,因此可根据原台阶构成的直角三角形来求出台阶的垂直高度.这样,就能求出改后的台阶的长,也就能求出增加了多少.
(2)修改前后的台阶构成的两个直角三角形中,已知了坡角,又求得了台阶的垂直高度,那么他们的水平距离就都能求出了,多占的地面的长度其实就是这两个水平距离的差.
解答 解:(1)如图,在Rt△ABC中,AC=AB•sin44°=5sin44°≈3.473(米).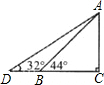
在Rt△ACD中,AD=$\frac{AC}{sin32°}$≈6.554(米),∴AD-AB=6.554-5≈1.55(米).
答:改善后的台阶会加长1.55米.
(2)如图,在Rt△ABC中,BC=AB•cos44°=5cos44°≈3.597(米).
在Rt△ACD中,CD=$\frac{AC}{tan32°}$≈5.558(米).
∴BD=CD-BC=5.558-3.597≈1.96(米).
答:改善后的台阶多占1.96米长的一段地面.
点评 本题是将实际问题转化为直角三角形中的数学问题,可把条件和问题放到直角三角形中,进行解决.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
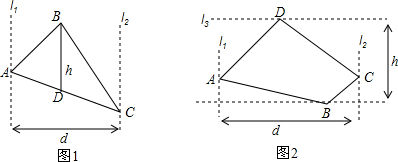
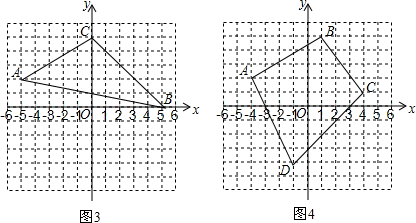
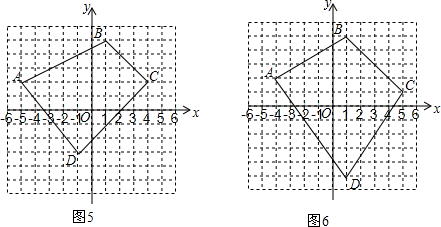
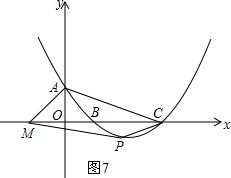
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
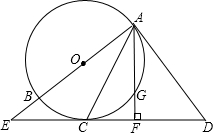 如图,AB是⊙O的直径,直线AD与⊙O相切于点A,点C在⊙O上,∠DAC=∠ACD,直线DC与AB的延长线交于点E.AF⊥ED于点F,交⊙O于点G.
如图,AB是⊙O的直径,直线AD与⊙O相切于点A,点C在⊙O上,∠DAC=∠ACD,直线DC与AB的延长线交于点E.AF⊥ED于点F,交⊙O于点G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
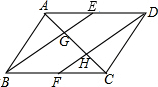 如图,?ABCD中,E,F分别是边AD,BC中点,AC分别交BE,DF于点G,H,请判断下列结论中正确的有( )
如图,?ABCD中,E,F分别是边AD,BC中点,AC分别交BE,DF于点G,H,请判断下列结论中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一组数据8,8,7,10,6,8,9的众数和中位数都是8 | |
| B. | 为了解全国中学生的心理健康情况,应该采用普查的方式 | |
| C. | 一个游戏的中奖概率是0.1,则做10次这样的游戏一定会中奖 | |
| D. | 若甲组数据的方差s2=0.01,乙组数据的方差s2=0.1,则乙组数据比甲组数据稳定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
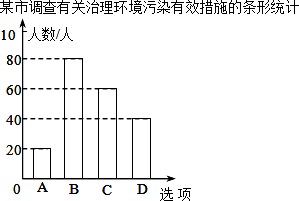 某市对市民进行了有关“治理环境污染”的问卷调查,调查问卷内容是“你认为下列哪种治理环境污染的措施最有效?”有以下四个选项(每份调查问卷必答且只选一个选项):
某市对市民进行了有关“治理环境污染”的问卷调查,调查问卷内容是“你认为下列哪种治理环境污染的措施最有效?”有以下四个选项(每份调查问卷必答且只选一个选项):查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com