
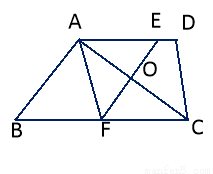
如图,在四边形ABCD中,AD∥BC,对角线AC的中点为O,过点O作AC的垂直平分线分别与AD、BC相交于点E、F,连接AF.求证:AE=AF。
科目:初中数学 来源:2015-2016学年江西省抚州市八年级上学期期末考试数学数学试卷(解析版) 题型:解答题
探索与研究:
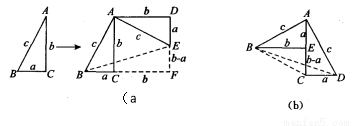
方法1:如图(a),对任意的符合条件的直角三角形绕其锐角顶点旋转90°所得,所以
∠BAE=90°,且四边形ACFD是一个正方形,它的面积和四边形ABFE面积相等,而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和,根据图示写出证明勾股定理的过程;
方法2:如图(b),是任意的符合条件的两个全等的Rt△BEA和Rt△ACD拼成的,你能根据图示再写一种证明勾股定理的方法吗?
查看答案和解析>>
科目:初中数学 来源:2015-2016学年江西省抚州市八年级上学期期末考试数学数学试卷(解析版) 题型:选择题
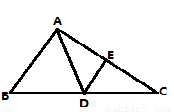
如图,DE是△ABC中边AC的垂直平分线,若BC=18 cm, AB=10 cm,则△ABD的周长为( )
A.16 cm B.18 cm C.26 cm D.28 cm
查看答案和解析>>
科目:初中数学 来源:2016届江苏省扬州市九年级下学期第一次月考数学试卷(解析版) 题型:解答题
【问题情境】一节数学课后,老师布置了一道课后练习题:
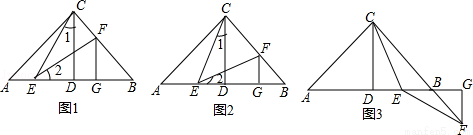
如图:已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,点E、F分别在A和BC上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF.
(1)阅读理解,完成解答
本题证明的思路可用下列框图表示:
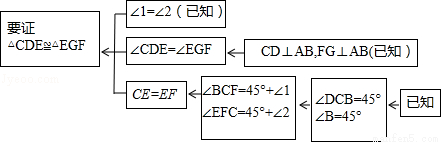
根据上述思路,请你完整地书写这道练习题的证明过程;
(2)特殊位置,证明结论
若CE平分∠ACD,其余条件不变,求证:AE=BF;
(3)知识迁移,探究发现
如图,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上且满足EC=EF,请直接写出AE与BF的数量关系.(不必写解答过程)
查看答案和解析>>
科目:初中数学 来源:2016届江苏省扬州市九年级下学期第一次月考数学试卷(解析版) 题型:填空题
如图,李明打网球时,球恰好打过网,且落在离网 4m 的位置上,则网球的击球的高度 h为 m.

查看答案和解析>>
科目:初中数学 来源:2015-2016学年江苏省扬州市七年级下学期第一次月考数学卷(解析版) 题型:填空题
(6分)已知:如图,AD⊥BC于D,EG⊥BC与G,∠E=∠3,试问:AD是∠BAC的平分线吗?若是,请说明理由.(在横线上填写正确的依据或证明步骤)
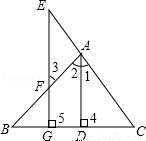
解答:是,理由如下:
∵AD⊥BC,EG⊥BC(已知)
∴∠4=∠5=90°(垂直的定义)
∴AD∥EG
∴∠1=∠E
∠2=∠3
∵∠E=∠3(已知)
∴∠ =∠ ;
∴AD是∠BAC的平分线(角平分线的定义).
查看答案和解析>>
科目:初中数学 来源:2015-2016学年江苏省扬州市八年级下学期第一次月考数学卷(解析版) 题型:选择题
口ABCD中,∠A︰∠B︰∠C︰∠D可以为( )
A、1︰2︰3︰4 B、1︰2︰2︰1 C、2︰2︰1︰1 D、2︰1︰2︰1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com