Question

9．在正方形ABCD中，对角线AC、BD交于点O，动点P在线段BC上（不含点B），∠BPE=$\frac{1}{2}$∠ACB，PE交BO于点E，过点B作BF⊥PE，垂足为F，交AC于点G．

（1）当点P与点C重合时（如图①），求证：△BOG≌△POE；
（2）通过观察、测量、猜想：$\frac{BF}{PE}$=$\frac{1}{2}$，并结合图②证明你的猜想；
（3）把正方形ABCD改为菱形，其他条件不变（如图③），若∠ACB=α，求$\frac{BF}{PE}$的值．（用含α的式子表示）

Answer 1

分析 （1）由四边形ABCD是正方形，P与C重合，易证得OB=OP，∠BOC=∠BOG=90°，由同角的余角相等，证得∠GBO=∠EPO，则可利用ASA证得：△BOG≌△POE；
（2）首先过P作PM∥AC交BG于M，交BO于N，易证得△BMN≌△PEN（ASA），△BPF≌△MPF（ASA），即可得BM=PE，BF=$\frac{1}{2}$BM．则可求得 $\frac{BF}{PE}$的值；
（3）首先过P作PM∥AC交BG于点M，交BO于点N，由（2）同理可得：BF=$\frac{1}{2}$BM，∠MBN=∠EPN，继而可证得：△BMN∽△PEN，然后由相似三角形的对应边成比例，求得$\frac{BF}{PE}$．

解答 （1）证明：∵四边形ABCD是正方形，P与C重合，
∴OB=OP，∠BOC=∠BOG=90°，
∵PF⊥BG，∠PFB=90°，
∴∠GBO=90°-∠BGO，∠EPO=90°-∠BGO，
∴∠GBO=∠EPO，
在△BOG和△POE中，$\left\{\begin{array}{l}{∠GBO=∠EPO}\\{OB=OP}\\{∠BOG=∠COE}\end{array}\right.$，
∴△BOG≌△POE（ASA）；

（2）解：猜想 $\frac{PF}{PE}$=$\frac{1}{2}$．
证明：如图2，过P作PM∥AC交BG于M，交BO于N，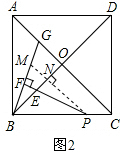
∴∠PNE=∠BOC=90°，∠BPN=∠OCB．
∵∠OBC=∠OCB=45°，
∴∠NBP=∠NPB．
∴NB=NP．
∵∠MBN=90°-∠BMN，∠NPE=90°-∠BMN，
∴∠MBN=∠NPE，
在△BMN和△PEN中，$\left\{\begin{array}{l}{∠MBN=∠NPE}\\{NB=NP}\\{∠MNB=∠PNE}\end{array}\right.$，
∴△BMN≌△PEN（ASA），
∴BM=PE．
∵∠BPE=$\frac{1}{2}$∠ACB，∠BPN=∠ACB，
∴∠BPF=∠MPF．
∵PF⊥BM，
∴∠BFP=∠MFP=90°．
在△BPF和△MPF中，$\left\{\begin{array}{l}{∠BPF=∠MPE}\\{PF=PF}\\{∠PFB=∠PFM}\end{array}\right.$，
∴△BPF≌△MPF（ASA）．
∴BF=MF．
即BF=$\frac{1}{2}$BM．
∴BF=$\frac{1}{2}$PE．
即 $\frac{BF}{PE}=\frac{1}{2}$；
故答案为$\frac{1}{2}$；
（3）解：如图3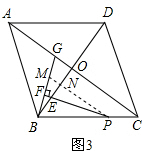，过P作PM∥AC交BG于点M，交BO于点N，
∴∠BPN=∠ACB=α，∠PNE=∠BOC=90°．
由（2）同理可得BF=$\frac{1}{2}$BM，∠MBN=∠EPN，
∴△BMN∽△PEN，
∴$\frac{BM}{PE}=\frac{BN}{PN}$．
在Rt△BNP中，tanα=$\frac{BN}{PN}$，
∴$\frac{BM}{PE}$=tanα．即$\frac{2BF}{PE}$=tanα．
∴$\frac{BF}{PE}=\frac{1}{2}$tanα．

点评 此题考查了正方形的性质、菱形的性质、相似三角形的判定与性质、全等三角形的判定与性质以及三角函数的定义等知识．此题综合性很强，难度较大，注意准确作出辅助线是解此题的关键，注意数形结合思想的应用．