
【题目】已知函数![]() 是关于x的二次函数,求:
是关于x的二次函数,求:
(1)满足条件m的值。
(2)m为何值时,抛物线有最底点?求出这个最底点的坐标,这时![]() 为何值时y随
为何值时y随![]() 的增大而增大?
的增大而增大?
(3)m为何值时,抛物线有最大值?最大值是多少?这时![]() 为何值时,y随
为何值时,y随![]() 的增大而减小.
的增大而减小.
【答案】(1) ![]() (2)m=2,(0,0) (3)见解析
(2)m=2,(0,0) (3)见解析
【解析】试题分析:
(1) 对照题目中所给出的二次函数解析式与二次函数的一般形式容易得到m的取值需要满足的条件. 综合考虑能够同时满足这些条件的m的取值即可.
(2) 根据二次函数的图象与性质易知,当抛物线开口向上时有最低点,且抛物线的开口方向由(m+2)的符号确定. 利用这一规律可以得到满足题意的m的取值范围,再结合第(1)小题的结论即可确定m的取值. 利用m的取值可以得到二次函数的具体解析式,不难得到抛物线最低点的坐标. 根据二次函数的图象与性质易知,抛物线开口向上时,在对称轴右侧y随x的增大而增大.
(3) 根据二次函数的图象与性质易知,当抛物线开口向下时有最大值. 仿照第(2)小题的思路即可得解.
试题解析:
(1) 对照该函数解析式![]() 与二次函数的一般形式y=ax2+bx+c (a≠0)可知,m的取值应该同时满足下列两个条件:
与二次函数的一般形式y=ax2+bx+c (a≠0)可知,m的取值应该同时满足下列两个条件:
![]() ,
,
解上述不等式,得 m≠-2,
解上述一元二次方程,得 m1=2,m2=-3,
因此,满足条件的m值为2或-3.
(2) 由二次函数的图象与性质可知:当m+2>0时,抛物线开口向上,有最低点.
故m的取值应该满足:m+2>0,即m>-2,
结合第(1)小题的结论得,当m=2时,抛物线有最低点.
当m=2时,二次函数的解析式为:y=4x2,故该抛物线最低点的坐标为(0, 0).
由于二次函数y=4x2图象的对称轴为y轴,即直线x=0,且抛物线开口向上,故当x>0时y随x的增大而增大.
综上所述,当m=2时,抛物线有最低点,最低点的坐标为(0, 0);当x>0时,y随x的增大而增大.
(3) 由二次函数的图象与性质可知:当m+2<0时,抛物线开口向下,有最大值.
故m的取值应该满足:m+2<0,即m<-2,
结合第(1)小题的结论得,当m=-3时,抛物线有最大值.
当m=-3时,二次函数的解析式为:y=-x2,
故当x=0时,该抛物线取得最大值,最大值为0.
由于二次函数y=-x2图象的对称轴为y轴,即直线x=0,且抛物线开口向下,故当x>0时y随x的增大而减小.
综上所述,当m=-3时,抛物线有最大值,最大值为0;当x>0时,y随x的增大而减小.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从C点沿抛物线向A点运动(点P不与点A重合),过点P作PD∥y轴交直线AC于点D.
(1)求抛物线的解析式;
(2)求点P在运动的过程中线段PD长度的最大值;
(3)在抛物线对称轴上是否存在点M,使|MA-MC|最大?若存在,请求出点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.
⑴请你补全这个输水管道的圆形截面;
⑵若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的三角形为整点三角形.如图,已知整点A(2,3),B(4,4),请在所给网格区域(含边界)上按要求画整点三角形.
(1)在图1中画一个△PAB,使点P的横、纵坐标之和等于点A的横坐标;
(2)在图2中画一个△PAB,使点P,B横坐标的平方和等于它们纵坐标和的4倍.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图所示的方格纸中每个小方格都是边长为1个单位长度的正方形,在平面直角坐标系中,已知点A(1,0),B(4,0),C(3,3),D(1,4).
(1)描出A、B、C、D、四点的位置,并顺次连接ABCD;
(2)四边形ABCD的面积是________.
(3)把四边形ABCD向左平移5个单位,再向上平移1个单位得到四边形A′B′C′D′,写出点A′、B′、C′、D′的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
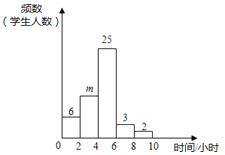
【题目】小强对自己所在班级的48名学生平均每周参加课外活动的时间进行了调查,由调查结果绘制了频数分布直方图,根据图中信息回答下列问题:
(1)求m的值;
(2)从参加课外活动时间在6~10小时的5名学生中随机选取2人,请你用列表或画树状图的方法,求其中至少有1人课外活动时间在8~10小时的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com