
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+![]() ��x�ύ��A����3��0����B��1��0�����㣮��y�ύ�ڵ�C����D���C���������ߵĶԳ���Գƣ�
��x�ύ��A����3��0����B��1��0�����㣮��y�ύ�ڵ�C����D���C���������ߵĶԳ���Գƣ�
��1���������ߵĽ���ʽ����ֱ��д����D�����ꣻ
��2����ͼ1����P�ӵ�A��������ÿ��1����λ���ȵ��ٶ���A��B�����˶��������Bʱֹͣ�˶�����APΪ�����ȱߡ�APQ����Q��x���Ϸ��������P���˶������У���APQ���ı���AOCD�ص����ֵ����ΪS����P���˶�ʱ��Ϊt�룬��S��t֮��ĺ�����ϵʽ��
��3����ͼ2������AC���ڵڶ������ڴ��ڵ�M��ʹ����M��O��AΪ��������������AOC���ƣ���ֱ��д�����з��������ĵ�M���꣮
���𰸡�
��1��
�⣺��������y=ax2+bx+![]() ����A����3��0����B��1��0�����㣬
����A����3��0����B��1��0�����㣬
��![]() ��
��
���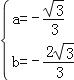 ��
��
�������߽���ʽΪy=��![]() x2��
x2��![]() x+
x+![]() ��
��
��D����������2��![]() ����
����
��2��
�⣺�ߵ�D��A���������1��������֮��Ϊ![]() ����tan��DAP=
����tan��DAP=![]() ��
��
���DAP=60�㣬
�֡ߡ�APQΪ�ȱ������Σ�
���Qʼ����ֱ��AD���˶�������Q��D�غ�ʱ���ɵȱ������ε����ʿ�֪��
AP=AD=![]() =2��
=2��
�ٵ�0��t��2ʱ��P���߶�AO�ϣ���ʱ��APQ��������ǡ�APQ���ı���AOCD���ص������
AP=t��
�ߡ�QAP=60�㣬
���Q��������Ϊtsin60��=![]() t��
t��
��S=![]() ��
��![]() t��t=
t��t=![]() t2��
t2��
�ڵ�2��t��3ʱ����ͼ��
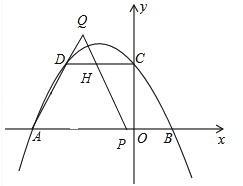
��ʱ��Q��AD���ӳ����ϣ���P��OA�ϣ�
��QP��DC���ڵ�H��
��DC��AP��
���QDH=��QAP=��QHD=��QPA=60�㣬
���QDH�ǵȱ������Σ�
��S=S��QAP��S��QDH��
��QA=t��
��S��QAP=![]() t2��
t2��
��QD=t��2��
��S��QDH=![]() ��t��2��2��
��t��2��2��
��S=![]() t2��
t2��![]() ��t��2��2=
��t��2��2=![]() t��
t��![]() ��
��
�۵�3��t��4ʱ����ͼ��
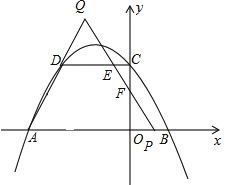
��ʱ��Q��AD���ӳ����ϣ���P���߶�OB�ϣ�
��QP��DC���ڵ�E����OC���ڵ�F������Q��AP�Ĵ��ѣ�����ΪG��
��OP=t��3����FPO=60�㣬
��OF=OPtan60��=![]() ��t��3����
��t��3����
��S��FOP=![]() ��
��![]() ��t��3����t��3��=
��t��3����t��3��=![]() ��t��3��2��
��t��3��2��
��S=S��QAP��S��QDE��S��FOP��S��QAP��S��QDE=![]() t��
t��![]() ��
��
��S=![]() t��
t��![]() ��
��![]() ��t��3��2=��
��t��3��2=��![]() t2+4
t2+4![]() t��
t��![]()
![]() ��
��
����������S��t֮��ĺ�����ϵʽΪS=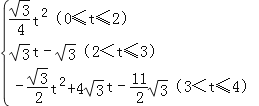 ��
��
��3��
�⣺��OC=![]() ��OA=3��OA��OC�����OAC�Ǻ�30���ֱ�������Σ�
��OA=3��OA��OC�����OAC�Ǻ�30���ֱ�������Σ�
�ٵ���AMO�ԡ�AMOΪֱ�ǵ�ֱ��������ʱ����ͼ��
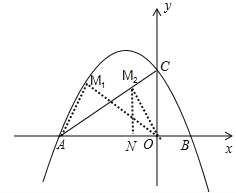
����M2��AO�Ĵ��ߣ�����ΪN��
�ߡ�M2AO=30�㣬AO=3��
��M2O=![]() ��
��
�֡ߡ�OM2N=M2AO=30�㣬
��ON=![]() OM2=
OM2=![]() ��M2N=
��M2N=![]() ON=
ON=![]() ��
��
��M2����������![]() ��
��![]() ����
����
ͬ���ɵ�M1������Ϊ����![]() ��
��![]() ����
����
�ڵ���AMO�ԡ�OAMΪֱ�ǵ�ֱ��������ʱ����ͼ��
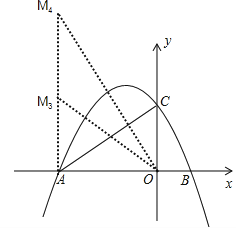
����M��O��AΪ��������������OAC���ƣ�
��![]() =
=![]() ����
����![]() =
=![]() ��
��
��OA=3��
��AM=![]() ��AM=3
��AM=3![]() ��
��
��AM��OA���ҵ�M�ڵڶ����ޣ�
���M����������3��![]() ����3��3
����3��3![]() ����
����
�������������������ĵ�M�����п��ܵ�����Ϊ����3��![]() ��������3��3
��������3��3![]() ��������
��������![]() ��
��![]() ��������
��������![]() ��
��![]() ����
����
����������1��ֱ�Ӵ�����ú�������ʽ���ɣ��ɵ�D��C�Գ���õ�D���꼴�ɣ�
��2��������ǵ����Ǻ���ֵ�ó���DAP=60�㣬���Qһֱ��ֱ��AD���˶����ֱ�̽�ֵ���P���߶�AO�ϣ���Q��AD���ӳ����ϣ���P���߶�OB���Լ���Q��AD���ӳ����ϣ���P���߶�OB��ʱ���ص���������������ε�������㹫ʽ��ô𰸼��ɣ�
��3������OC=![]() ��OA=3��OA��OC�����OAC�Ǻ�30���ֱ�������Σ����������̽�֣�����AMO�ԡ�AMOΪֱ�ǵ�ֱ��������ʱ������AMO�ԡ�OAMΪֱ�ǵ�ֱ��������ʱ���ó��𰸼��ɣ�
��OA=3��OA��OC�����OAC�Ǻ�30���ֱ�������Σ����������̽�֣�����AMO�ԡ�AMOΪֱ�ǵ�ֱ��������ʱ������AMO�ԡ�OAMΪֱ�ǵ�ֱ��������ʱ���ó��𰸼��ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD�ǡ�ABC�Ľ�ƽ���ߣ���ADΪ�ҵġ�O��AB��AC��E��F����֪EF��BC��
��1����֤��BC�ǡ�O�����ߣ�
��2������֪AE=12��CF=6����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ϊ�˽�������������������ë���ƹ���������������˶���Ŀ��ϲ���������������չ�ˡ�����ϲ���������˶���Ŀ����������飨ÿλ�������߱�����ֻ��ѡ����ϲ����һ�������˶���Ŀ��������������������ͳ�ƣ����Ƴ�����ͼ��ʾ��������������ͳ��ͼ��
��1��������������
��2�������������ͳ��ͼ����������
��3����������ϲ�������������˶���Ŀ��������Լ��4000�ˣ�������Ƹ�����ϲ����ë���˶���Ŀ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������·�г��ѳ�Ϊ�й��˳��е���Ҫ��ͨ���ߣ���ƽ���ٶ�����ͨ��·�г�ƽ���ٶȵ�3����ͬ����ʻ690km��������·�г�����ͨ��·�г���������4.6h���������·�г���ƽ���ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������ͬѧijѧ�ڵ��Ĵ���ѧ���Գɼ�����λ���֣����±���
��һ�� | �ڶ��� | ������ | ���Ĵ� | |
�� | 87 | 95 | 85 | 93 |
�� | 80 | 80 | 90 | 90 |
���ϱ����㣬�ס�������ͬѧ�Ĵ���ѧ���Գɼ��ķ���ֱ�ΪS��2=17��S��2=25������˵����ȷ���ǣ�������
A.��ͬѧ�Ĵ���ѧ���Գɼ���ƽ������89��
B.��ͬѧ�Ĵ���ѧ���Գɼ�����λ����90��
C.��ͬѧ�Ĵ���ѧ���Գɼ���������80��
D.��ͬѧ�Ĵ���ѧ���Գɼ����ȶ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC����C=90�㣬AC=BC=a���ڡ�ABC�нس�һ��������A1B1C1D1 �� ʹ��A1 �� D1�ֱ���AC��BC���ϣ���B1C1��AB���ϣ��ڡ�BC1D1�ڽس��ڶ���������A2B2C2D2 �� ʹ��A2 �� D2�ֱ���BC1 �� D1C1���ϣ���B2C2��BD1���ϣ��������˷�������ȥ�����n�������εı߳�Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�AB=AC����F��BC�ӳ�����һ�㣬��CFΪ�ߣ�������CDEF��ʹ����CDEF���A��BC��ͬ�࣬����BE����G��BE���е㣬����AG��DG��
��1����ͼ�٣�����BAC=��DCF=90��ʱ��ֱ��д��AG��DG��λ�ú�������ϵ��
��2����ͼ�ڣ�����BAC=��DCF=60��ʱ����̽��AG��DG��λ�ú�������ϵ��
��3������BAC=��DCF=��ʱ��ֱ��д��AG��DG��������ϵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com