
����Ŀ���ڡ�ABC�У�AB=AC����F��BC�ӳ�����һ�㣬��CFΪ�ߣ�������CDEF��ʹ����CDEF���A��BC��ͬ�࣬����BE����G��BE���е㣬����AG��DG��
��1����ͼ�٣�����BAC=��DCF=90��ʱ��ֱ��д��AG��DG��λ�ú�������ϵ��
��2����ͼ�ڣ�����BAC=��DCF=60��ʱ����̽��AG��DG��λ�ú�������ϵ��
��3������BAC=��DCF=��ʱ��ֱ��д��AG��DG��������ϵ��
���𰸡�
��1��
�⣺AG��DG��AG=DG��
֤�����ӳ�DG��BC����H������AH��AD��
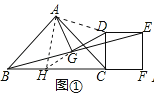
���ı���DCEF�������Σ�
��DE=DC��DE��CF��
���GBH=��GED����GHB=��GDE��
��G��BC���е㣬
��BG=EG��
�ڡ�BGH�͡�EGD��
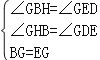
���BGH�ա�EGD��AAS����
��BH=ED��HG=DG��
��BH=DC��
��AB=AC����BAC=90�㣬
���ABC=��ACB=45�㣬
�ߡ�DCF=90�㣬
���DCB=90�㣬
���ACD=45�㣬
���ABH=��ACD=45�㣬
�ڡ�ABH�͡�ACD��

���ABH�ա�ACD��SAS����
���BAH=��CAD��AH=AD��
�ߡ�BAH+��HAC=90�㣬
���CAD+��HAC=90�㣬����HAD=90�㣬
��AG��GD��AG=GD��
��2��
�⣺AG��GD��AG=![]() DG��
DG��
֤�����ӳ�DG��BC����H������AH��AD��

���ı���DCEF�������Σ�
��DE=DC��DE��CF��
���GBH=��GED����GHB=��GDE��
��G��BC���е㣬
��BG=EG��
�ڡ�BGH�͡�EGD��

���BGH�ա�EGD��AAS����
��BH=ED��HG=DG��
��BH=DC��
��AB=AC����BAC=��DCF=60��
���ABC=60�㣬��ACD=60�㣬
���ABC=��ACD=60�㣬
�ڡ�ABH�͡�ACD��

���ABH�ա�ACD��SAS����
���BAH=��CAD��AH=AD��
���BAC=��HAD=60�㣻
��AG��HD����HAG=��DAG=30�㣬
��tan��DAG=tan30��=![]() =
=![]() ��
��
��AG=![]() DG��
DG��
��3��
�⣺DG=AGtan![]() ��
��
֤�����ӳ�DG��BC����H������AH��AD��

���ı���DCEF�������Σ�
��DE=DC��DE��CF��
���GBH=��GED����GHB=��GDE��
��G��BC���е㣬
��BG=EG��
�ڡ�BGH�͡�EGD��
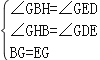
���BGH�ա�EGD��AAS����
��BH=ED��HG=DG��
��BH=DC��
��AB=AC����BAC=��DCF=����
���ABC=90�㩁![]() ����ACD=90�㩁
����ACD=90�㩁![]() ��
��
���ABC=��ACD��
�ڡ�ABH�͡�ACD��
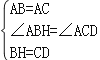
���ABH�ա�ACD��SAS����
���BAH=��CAD��AH=AD��
���BAC=��HAD=����
��AG��HD����HAG=��DAG=![]() ��
��
��tan��DAG=tan![]() =
=![]() ��
��
��DG=AGtan![]() ��
��
����������1���ӳ�DG��BC����H������AH��AD��ͨ��֤�á�BGH�ա�EGD���BH=ED��HG=DG���ó�BH=DC��Ȼ��֤�á�ABH�ա�ACD���ó���BAH=��CAD��AH=AD��������á�HAD=90�㣬�������AG��GD��AG=GD��
��2���ӳ�DG��BC����H������AH��AD��ͨ��֤�á�BGH�ա�EGD���BH=ED��HG=DG���ó�BH=DC��Ȼ��֤�á�ABH�ա�ACD���ó���BAH=��CAD��AH=AD��������á�HAD�ǵȱ������Σ�����֤��AG��GD��AG=![]() DG��
DG��
��3���ӳ�DG��BC����H������AH��AD��ͨ��֤�á�BGH�ա�EGD���BH=ED��HG=DG���ó�BH=DC��Ȼ��֤�á�ABH�ա�ACD���ó���BAH=��CAD��AH=AD��������á�HAD�ǵ��������Σ�����֤��DG=AGtan![]() ��
��
�����㾫����ͨ��������õ��������ε����ʺ����ε����ʣ����յ��������ε���������ȣ���ƣ��ȱ߶ԵȽǣ������ε������߶���ȣ����εĶԽ����ഹֱ������ÿһ���Խ���ƽ��һ��Խǣ����α������Խ��߷ֳ��ĸ�ȫ�ȵ�ֱ�������Σ����ε�������������Խ��߳��Ļ���һ�뼴���Խ����⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+![]() ��x�ύ��A����3��0����B��1��0�����㣮��y�ύ�ڵ�C����D���C���������ߵĶԳ���Գƣ�
��x�ύ��A����3��0����B��1��0�����㣮��y�ύ�ڵ�C����D���C���������ߵĶԳ���Գƣ�
��1���������ߵĽ���ʽ����ֱ��д����D�����ꣻ
��2����ͼ1����P�ӵ�A��������ÿ��1����λ���ȵ��ٶ���A��B�����˶��������Bʱֹͣ�˶�����APΪ�����ȱߡ�APQ����Q��x���Ϸ��������P���˶������У���APQ���ı���AOCD�ص����ֵ����ΪS����P���˶�ʱ��Ϊt�룬��S��t֮��ĺ�����ϵʽ��
��3����ͼ2������AC���ڵڶ������ڴ��ڵ�M��ʹ����M��O��AΪ��������������AOC���ƣ���ֱ��д�����з��������ĵ�M���꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У���E��F�ֱ��ڱ�BC��CD�ϣ����AE=4��EF=3��AF=5����ô������ABCD��������� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���ACΪֱ���ġ�O���AB���ڵ�D����EΪ��O��һ�㣬����CE���ӳ���AB�ڵ�F������ED��
��1������B+��FED=90�㣬��֤��BC�ǡ�O�����ߣ�
��2����FC=6��DE=3��FD=2�����O��ֱ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���мƻ�����һЩ�ز�������ǰ��Χ�ơ�A�����а��棬B������᭸ɶ�����C���������ɺ�Ѽ����D���˳Ǻ����ӻ����������ز�����ȫ�з�Χ�������ȡ�˲�����������ʾ����飺������ϲ�����ز���ʲô��������ѡ��ֻѡһ�֣����ֽ��������������Ƴ���ͼ��ʾ�IJ�����������ͳ��ͼ������ͳ��ͼ��
��1���벹ȫ����ͳ��ͼ������ͳ��ͼ��
��2����ȫ����280��������ȫ����ϲ��������᭸ɶ�����������Լ�ж������ˣ�
��3����һ�������Ŀڴ������ĸ��ֱ�д�������ز����A��B��C��D��С���������ȫ��ͬ�����������һ��С��Ȼ��Żأ����ҡ�Ⱥ����������һ��С�������ζ�������A���ĸ���Ϊ_____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC��ƽ��ֱ������ϵ�ڣ����������ֱ�ΪA����1��5����B����4��1����C����1��1������ABC�Ƶ�A��ʱ����ת90�㣬�õ���AB��C�䣬��B��C�Ķ�Ӧ��ֱ�Ϊ��B�䣬C�䣬
��1��������AB��C�䣻
��2��д����B�䣬C������ꣻ
��3������ڡ�ABC��ת�Ĺ����У���C������·������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ԭ��O��ֱ��AB�뷴��������![]() ��k��0����ͼ����A��B���㣬��B����Ϊ����2��m��������A��AC��y���ڵ�C��OA�Ĵ�ֱƽ����DE��OC�ڵ�D����AB�ڵ�E������ACD���ܳ�Ϊ5����k��ֵΪ.
��k��0����ͼ����A��B���㣬��B����Ϊ����2��m��������A��AC��y���ڵ�C��OA�Ĵ�ֱƽ����DE��OC�ڵ�D����AB�ڵ�E������ACD���ܳ�Ϊ5����k��ֵΪ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵깺��һ����Ʒ��ÿ����Ʒ����30Ԫ�������з���������Ʒÿ���������y��������ÿ�����ۼ�x��Ԫ���Ĺ�ϵ�������£�
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
��1����֪y��x����һ�κ�����ϵ�������ϱ������y��x֮��Ĺ�ϵʽ����д���Ա���x��ȡֵ��Χ����
��2������̵�����������Ʒ��ÿ��Ҫ���150Ԫ������ôÿ����Ʒ�����ۼ�Ӧ��Ϊ����Ԫ��
��3������̵�ÿ������������Ʒ��������Ϊw��Ԫ�������w��x֮��Ĺ�ϵʽ�������ÿ����Ʒ���ۼ۶�Ϊ����Ԫʱ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������C��y2=4x�Ľ���ΪF����Ϊl����F��C����A��B���㣬��x��ĸ����ύ�ڵ�P�� ��������F��l���صõ��ҳ�Ϊ ![]() ����|AB|��
����|AB|��
�����ж�ֱ��PA��C�Ľ����������˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com