能判定四边形ABCD为平行四边形的条件是( )A．AB=AD.CB=CDB．∠A=∠B.∠C=∠DC．AB=CD.AD=BCD．AB∥CD.AD=BC 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

15．能判定四边形ABCD为平行四边形的条件是（　　）

A．

AB=AD，CB=CD

B．

∠A=∠B，∠C=∠D

C．

AB=CD，AD=BC

D．

AB∥CD，AD=BC

分析平行四边形的五种判定方法分别是：（1）两组对边分别平行的四边形是平行四边形；（2）两组对边分别相等的四边形是平行四边形；（3）一组对边平行且相等的四边形是平行四边形；（4）两组对角分别相等的四边形是平行四边形；（5）对角线互相平分的四边形是平行四边形．根据平行四边形的判定方法，采用排除法，逐项分析判断．

解答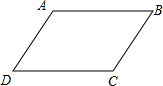解：A、若AB=AD，CB=CD，无法判定，四边形ABCD为平行四边形，故此选项错误；
B、∠A=∠B，∠C=∠D，无法判定，四边形ABCD为平行四边形，故此选项错误；
C、AB=CD，AD=BC，可判定是平行四边形的条件，故此选项正确；
D、此条件下无法判定四边形的形状，还可能是等腰梯形，故此选项错误．
故选：C．

点评本题考查了平行四边形的判定，平行四边形的判别方法是说明一个四边形为平行四边形的理论依据，在应用判定定理判定平行四边形时，应仔细观察题目所给的条件，仔细选择适合于题目的判定方法进行解答，避免混用判定方法．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

5．阅读下面材料：
学习了三角形全等的判定方法（即“SAS”、“ASA”、“AAS”、“SSS”）和直角三角形全等的判定方法（即“HL”）后，小聪继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究．
小聪将命题用符号语言表示为：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E．
小聪想：要想解决问题，应该对∠B进行分类研究．
∠B可分为“直角、钝角、锐角”三种情况进行探究．
第一种情况：当∠B是直角时，如图1，在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E=90°，根据“HL”定理，可以知道Rt△ABC≌Rt△DEF．
第二种情况：当∠B是锐角时，如图2，BC=EF，∠B=∠E＜90°，在射线EM上有点D，使DF=AC，画出符合条件的点D，则△ABC和△DEF的关系是C；
A．全等 B．不全等 C．不一定全等
第三种情况：当∠B是钝角时，如图3，在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E＞90°，求证：△ABC≌△DEF．