
【题目】如图1,已知□ABCD,AB//x轴,AB=6,点A的坐标为(1,-4),点D的坐标为(-3,4),点B在第四象限,点P是□ABCD边上的一个动点.

(1)若点P在边BC上,PD=CD,求点P的坐标.
(2)若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x-1上,求点P的坐标.
(3)若点P在边AB,AD,CD上,点G是AD与y轴的交点,如图2,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标(直接写出答案).
【答案】
(1)
解:在□ABCD中, CD=AB=6,
所以点P与点C重合,
所以点P的坐标为(3,4).
(2)
解:①当点P在边AD上时,
由已知得,直线AD的函数表达式为y=-2x-2,
设P(a,-2a-2),且-3≤a≤1,
若点P关于x轴对称点Q1(a,2a+2)在直线y=x-1上,
所以2a+2=a-1,解得a=-3,此时P(-3,4)。
若点P关于y轴对称点Q2(-a,-2a-2)在直线y=x-1上,
所以-2a-2=-a-1,解得a=-1,此时P(-1,0).
②当点P在边AB上时,设P(a,-4),且1≤a≤7,
若点P关于x轴对称点Q3(a,4)在直线y=x-1上,
所以4=a-1,解得a=5,此时P(5,-4).
若点P关于y轴对称点Q4(-a,-4)在直线y=x-1上,
所以-4=-a-1,解得a=3,此时P(3,-4).
综上所述,点P的坐标为(-3,4)或(-1,0)或(5,-4)或(3,-4).
(3)
解:因为直线AD为y=-2x-2,所以G(0,-2).
①如图,当点P在CD边上时,可设P(m,4),且-3≤m≤3,
则可得M′P=PM=4+2=6,M′G=GM=|m|,
易证得△OGM′~△HM′P,
则 ![]() ,
,
即 ![]() ,
,
则OM′= ![]() ,
,
在Rt△OGM′中,
由勾股定理得, ![]() ,
,
解得m= ![]() 或
或 ![]() ,
,
则P( ![]() ,4)或(
,4)或( ![]() ,4);
,4);
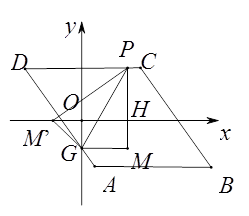
②如下图,当点P在AD边上时,设P(m,-2m-2),
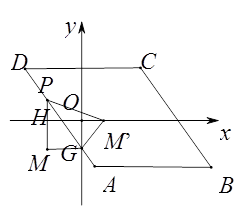
则PM′=PM=|-2m|,GM′=MG=|m|,
易证得△OGM′~△HM′P,
则 ![]() ,
,
即 ![]() ,
,
则OM′= ![]() ,
,
在Rt△OGM′中,
由勾股定理得, ![]() ,
,
整理得m= ![]() ,
,
则P( ![]() ,3);
,3);
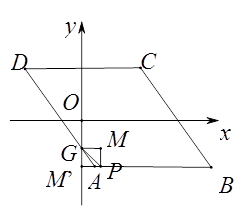
如下图,当点P在AB边上时,设P(m,-4),
此时M′在y轴上,则四边形PM′GM是正方形,
所以GM=PM=4-2=2,
则P(2,-4).
综上所述,点P的坐标为(2,-4)或( ![]() ,3)或(
,3)或( ![]() ,4)或(
,4)或( ![]() ,4).
,4).
【解析】(1)点P在BC上,要使PD=CD,只有P与C重合;(2)首先要分点P在边AB,AD上时讨论,根据“点P关于坐标轴对称的点Q”,即还要细分“点P关于x轴的对称点Q和点P关于y轴的对称点Q”讨论,根据关于x轴、y轴对称点的特征(关于x轴对称时,点的横坐标不变,纵坐标变成相反数;关于y轴对称时,相反;)将得到的点Q的坐标代入直线y=x-1,即可解答;(3)在不同边上,根据图象,点M翻折后,点M’落在x轴还是y轴,可运用相似求解.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.


科目:初中数学 来源: 题型:
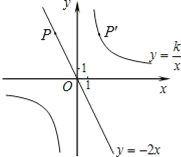
【题目】如图,已知直线y=﹣2x经过点P(﹣2,a),点P关于y轴的对称点P′在反比例函数![]() (k≠0)的图象上.
(k≠0)的图象上.
(1)求a的值;
(2)直接写出点P′的坐标;
(3)求反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAC=60°,AC与BC交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论中一定成立的是 . (把所有正确结论的序号都填在横线上) ①OG= ![]() AB;
AB;
②与△EGD全等的三角形共有5个;
③S四边形CDGF>S△ABF;
④由点A、B、D、E构成的四边形是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=BC=CD=AD,∠BAD=∠B=∠C=∠D=90°,点E、F分别在正方形ABCD的边DC、BC上,AG⊥EF且 AG=AB,垂足为G,则: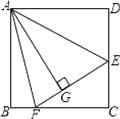
(1)△ABF与△ AGF全等吗?说明理由;
(2)求∠EAF的度数;
(3)若AG=4,△AEF的面积是6,求△CEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习三角形中位线的性质时,小亮对课本给出的解决办法进行了认真思考:
课本研究三角形中位线性质的方法
已知:如图①,已知△ABC中,D,E分别是AB,AC两边中点.求证:DE∥BC,DE=![]() BC.
BC.
证明:延长DE至点F,使EF=DE,连接FC.…则△ADE≌△CFE.∴…


请你利用小亮的发现解决下列问题:
(1)如图③,AD是△ABC的中线,BE交AC于点E,交AD于点F,且AE=EF,求证:AC=BF.

请你帮助小亮写出辅助线作法并完成论证过程:
(2)解决问题:如图⑤,在△ABC中,∠B=45°,AB=10,BC=8,DE是△ABC的中位线.过点D,E作DF∥EG,分别交BC于点F,G,过点A作MN∥BC,分别与FD,GE的延长线交于点M,N,则四边形MFGN周长的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.
(1)求证:△ADC≌△ECD;
(2)当点D在什么位置时,四边形ADCE是矩形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A、C坐标分别是(8,0),(0,4),反比例函数y=![]() (x>0)的图象过对角线的交点P并且与AB、BC分别交于D、E两点,连接OD、OE、DE,则△ODE的面积为( )
(x>0)的图象过对角线的交点P并且与AB、BC分别交于D、E两点,连接OD、OE、DE,则△ODE的面积为( )

A. 14 B. 12 C. 15 D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com