
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 为弦,
为弦,![]() ,
,![]() ,
,![]() .
.
![]() 求
求![]() ;
;
![]() 过
过![]() 点作
点作![]() ,交
,交![]() 于
于![]() 点,求
点,求![]() 的值.
的值.

【答案】![]() ;
;![]() .
.
【解析】
(1)作OF⊥DC于F,连结OD,根据垂径定理由OF⊥DC得DF=![]() DC=3.在Rt△ODF中,利用勾股定理可计算出OF=4,然后根据梯形的面积公式计算即可;
DC=3.在Rt△ODF中,利用勾股定理可计算出OF=4,然后根据梯形的面积公式计算即可;
(2)易证四边形ABCD是等腰梯形,作DG⊥AB于G,根据等腰梯形的性质得出DG=OF=4,AG=![]() (AB﹣CD)=2.在Rt△ADG中,由勾股定理得出AD=
(AB﹣CD)=2.在Rt△ADG中,由勾股定理得出AD=![]() =2
=2![]() ,再证明四边形ADCE是平行四边形,得出CE=AD=2
,再证明四边形ADCE是平行四边形,得出CE=AD=2![]() ,AE=CD=6,那么BE=AB﹣AE=4.然后根据S△BCE=
,AE=CD=6,那么BE=AB﹣AE=4.然后根据S△BCE=![]() BCCEsin∠BCE=
BCCEsin∠BCE=![]() BEDG,即可求出sin∠BCE=
BEDG,即可求出sin∠BCE=![]() .
.
(1)作OF⊥DC于F,连结OC,如图,∵OF⊥DC,∴CF=DF=![]() DC=
DC=![]() ×6=3.
×6=3.
∵直径AB=10,∴OD=5.在Rt△ODF中,OF=![]() =4,∴S四边形ABCD=
=4,∴S四边形ABCD=![]() ×(6+10)×4=32;
×(6+10)×4=32;

(2)∵CD∥AB,∴![]() =
=![]() ,∴AD=BC.
,∴AD=BC.
∵CD∥AB,CD<AB,∴四边形ABCD是等腰梯形.
作DG⊥AB于G,则DG=OF=4,AG=![]() (AB﹣CD)=2.在Rt△ADG中,由勾股定理得:AD=
(AB﹣CD)=2.在Rt△ADG中,由勾股定理得:AD=![]() =2
=2![]() ,∴BC=AD=2
,∴BC=AD=2![]() .
.
∵CE∥AD,CD∥AB,∴四边形ADCE是平行四边形,∴CE=AD=2![]() ,AE=CD=6,∴BE=AB﹣AE=4.
,AE=CD=6,∴BE=AB﹣AE=4.
∵S△BCE=![]() BCCEsin∠BCE=
BCCEsin∠BCE=![]() BEDG,∴
BEDG,∴![]() ×2
×2![]() ×2
×2![]() sin∠BCE=
sin∠BCE=![]() ×4×4,∴sin∠BCE=
×4×4,∴sin∠BCE=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】综合与实践
(1)实践操作:![]() 中,
中,![]() ,
,![]() 为直线
为直线![]() 上一点,过
上一点,过![]() 点作
点作![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,如图①,图②,图③所示,则
,如图①,图②,图③所示,则![]() 的形状为______.
的形状为______.
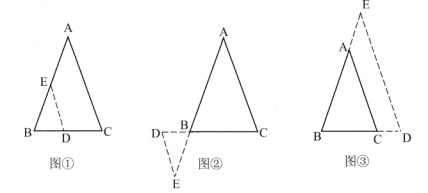
(2)问题解决:等腰三角形是一种特殊的三角形,常与全等三角形的相关知识结合在一起解决问题.如图④,![]() 中,
中,![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() 为
为![]() 延长线上一点,且
延长线上一点,且![]() ,
,![]() 交
交![]() 于
于![]() ,求证:
,求证:![]() .
.
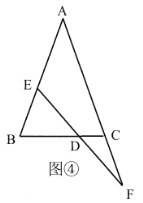
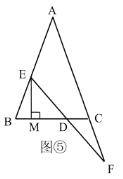
(3)拓展与应用,在(2)的条件下,如图⑤,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,若
,若![]() ,则
,则![]() 的长为______.
的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为数___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c过点A(0,2).
(1)若点(﹣![]() ,0)也在该抛物线上,求a,b满足的关系式;
,0)也在该抛物线上,求a,b满足的关系式;
(2)若该抛物线上任意不同两点M(x1,y1),N(x2,y2)都满足:当x1<x2<0时,(x1﹣x2)(y1﹣y2)>0;当0<x1<x2时,(x1﹣x2)(y1﹣y2)<0.以原点O为心,OA为半径的圆与拋物线的另两个交点为B,C,且△ABC有一个内角为60°.
①求抛物线的解析式;
②若点P与点O关于点A对称,且O,M,N三点共线,求证:PA平分∠MPN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b,c是△ABC的三条边,关于x的方程![]() x2+
x2+![]() x+c-
x+c-![]() a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
(1)试判断△ABC的形状;
(2)若a,b为方程x2+mx-3m=0的两个根,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前我国建立了比较完善的经济困难学生资助体系.某校去年上半年发放给每个经济困难学生389元,今年上半年发放了438元,设每半年发放的资助金额的平均增长率为![]() ,则下面列出的方程中正确的是( )
,则下面列出的方程中正确的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的例题,范例:解方程![]() ,
,
解:(1)当![]() ≥0时,原方程化为
≥0时,原方程化为![]() ,解得:
,解得:![]() ,
,![]() (不合题意,舍去).
(不合题意,舍去).
(2)当![]() <0时,原方程化为
<0时,原方程化为![]() ,解得:
,解得:![]() ,
,![]() (不合题意,舍去).
(不合题意,舍去).
∴原方程的根是![]() ,
,![]()
请参照例题解方程![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com