【题目】已知一次函数y=x+4的图象经过点（m，6），则m=_____．
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】在正方形ABCD中，BD是一条对角线，点P在CD上（与点C，D不重合），连接AP，平移△ADP，使点D移动到点C，得到△BCQ，过点Q作QM⊥BD于M，连接AM，PM（如图1）．
（1）判断AM与PM的数量关系与位置关系并加以证明；
（2）若点P在线段CD的延长线上，其它条件不变（如图2），（1）中的结论是否仍成立？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在研究圆的有关性质时，我们曾做过这样的一个操作“将一张圆形纸片沿着它的任意一条直径翻折，可以看到直径两侧的两个半圆互相重合”．由此说明（ ）
A. 圆是中心对称图形，圆心是它的对称中心
B. 圆是轴对称图形，任意一条直径所在的直线都是它的对称轴
C. 圆的直径互相平分
D. 垂直弦的直径平分弦及弦所对的弧
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，EF∥AD,∠1=∠2,∠B=35°,将求∠BDG的过程填写完整。
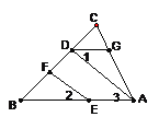
解： ∵EF∥AD，
∴∠2=____ (________________________________)
又∵∠1=∠2
∴∠1= ( 等量代换 )
∴DG∥_____ (___________________________________)
∴∠B+______=180°(___________________________)
∵∠B=35°
∴∠BDG =_______
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】倡导研究性学习方式，着力教材研究，习题研究，是学生跳出题海，提高学习能力和创新能力的有效途径．下面是一案例，请同学们认真阅读、研究，完成“类比猜想”及后面的问题．
习题解答
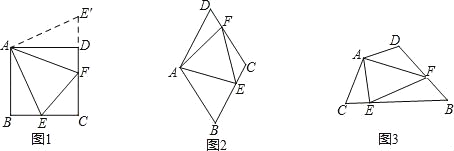
习题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，则EF=BE+DF，说明理由．
解：
∵正方形ABCD中，AB=AD，∠BAD=∠ADC=90°
∴把△ABE绕点A逆时针旋转90°至△ADE′，点F、D、E′在一条直线上．
∴∠E′AF=90°-45°=45°=∠EAF．
又∵AE′=AE，AF=AF
∴△AE′FF≌△AEF（SAS）
∴EF=E′F=DE′+DF=BE+DF．
习题研究．
观察分析：
观察图1，由解答可知，该题有用的条件是①．ABCD是四边形，点E、F分别在边BC、CD上；②．AB=AD；③．∠B=∠D=90°∠；④．∠EAF=
∠BAD．
类比猜想：
在四边形ABCD中，点E、F分别在BC、CD上，当AB=AD，∠B=∠D时，还有EF=BE+DF吗？
要解决上述问题，可从特例入手，请同学们思考：如图2，在菱形ABCD中，点E、F分别在BC、CD上，当∠BAD=120°，∠EAF=60°时，还有EF=BE+DF吗？试证明．
（2）在四边形ABCD中，点E、F分别在边BC、CD上，当AB=AD，∠B+∠D=180°，∠EAF=
∠BAD时，还有EF=BE+DF吗？使用图3证明．
归纳概括：
反思前面的解答，思考每个条件的作用，可以得到一个结论“EF=BE+DF”的一般命题： ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
