
【题目】在正方形ABCD中,BD是一条对角线,点P在CD上(与点C,D不重合),连接AP,平移△ADP,使点D移动到点C,得到△BCQ,过点Q作QM⊥BD于M,连接AM,PM(如图1).

(1)判断AM与PM的数量关系与位置关系并加以证明;
(2)若点P在线段CD的延长线上,其它条件不变(如图2),(1)中的结论是否仍成立?请说明理由.
【答案】(1)AM=PM,AM⊥PM.(2)成立,理由见解析.
【解析】
试题分析:(1)先判断出△DMQ是等腰直角三角形,再判断出△MDP≌△MQC(SAS),最后进行简单的计算即可;
(2)先判断出△DMQ是等腰直角三角形,再判断出△MDP≌△MQC(SAS),最后进行简单的计算即可.
试题解析:(1)连接CM,

∵四边形ABCD是正方形,QM⊥BD,
∴∠MDQ=45°,
∴△DMQ是等腰直角三角形.
∵DP=CQ,
在△MDP与△MQC中

∴△MDP≌△MQC(SAS),
∴PM=CM,∠MPC=∠MCP.
∵BD是正方形ABCD的对称轴,
∴AM=CM,∠DAM=∠MCP,
∴∠AMP=180°-∠ADP=90°,
∴AM=PM,AM⊥PM.
(2)成立,
理由如下:
连接CM,
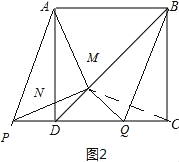
∵四边形ABCD是正方形,QM⊥BD,
∴∠MDQ=45°,
∴△DMQ是等腰直角三角形.
∵DP=CQ,
在△MDP与△MQC中

∴△MDP≌△MQC(SAS),
∴PM=CM,∠MPC=∠MCP.
∵BD是正方形ABCD的对称轴,
∴AM=CM,∠DAM=∠MCP,
∴∠DAM=∠MPC,
∵∠PND=∠ANM
∴∠AMP=∠ADP=90°
∴AM=PM,AM⊥PM.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】下列各式从左边到右边的变形是因式分解的是( )
A.(a+1)(a﹣1)=a2﹣1
B.a2﹣6a+9=(a﹣3)2
C.x2+2x+1=x(x+2x)+1
D.﹣18x4y3=﹣6x2y23x2y
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中一小岛有一个观测点A,某天上午观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.B处距离观测点30![]() 海里,若该渔船的速度为每小时30海里,问该渔船多长时间到达观测点A的北偏西60°方向上的C处?(计算结果用根号表示,不取近似值)
海里,若该渔船的速度为每小时30海里,问该渔船多长时间到达观测点A的北偏西60°方向上的C处?(计算结果用根号表示,不取近似值)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,直线![]() 经过点(2,3)和(-1,-3),直线
经过点(2,3)和(-1,-3),直线![]() 经过原点,且与直线
经过原点,且与直线![]() 交于点P(-2,a).
交于点P(-2,a).
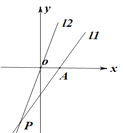
(1)求a的值.
(2)(-2,a)可看成怎样的二元一次方程组的解?
(3)设直线![]() 与x轴交于点A,你能求出△APO的面积吗?
与x轴交于点A,你能求出△APO的面积吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:(-2a2) ·(3ab2-5ab3)结果是( )
A. 6a3b2+10a3b3B. -6a3b2+10a2b3C. -6a3b2+10a3b3D. 6a3b2-10a3b3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com