
【题目】如图,海中一小岛有一个观测点A,某天上午观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.B处距离观测点30![]() 海里,若该渔船的速度为每小时30海里,问该渔船多长时间到达观测点A的北偏西60°方向上的C处?(计算结果用根号表示,不取近似值)
海里,若该渔船的速度为每小时30海里,问该渔船多长时间到达观测点A的北偏西60°方向上的C处?(计算结果用根号表示,不取近似值)

【答案】该渔船从B处开始航行(1+![]() )小时到达C处.
)小时到达C处.
【解析】
试题分析:过点A作AP⊥BC,垂足为P,在Rt△APB利用三角函数求的AP和PB的长,则在直角△APC中利用三角函数即可求得PC的长,即可求得BC的长,然后根据速度公式求解.
试题解析:过点A作AP⊥BC,垂足为P.
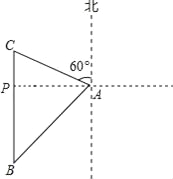
在Rt△APB中,∵∠APB=90°,∠PAB=45°,AB=30![]() ,
,
∴BP=AP=![]() AB=30
AB=30![]() .
.
在Rt△APC中,∵∠APC=90°,∠PAC=30°,
∴tan∠PAC=![]() ,
,
∴CP=APtan∠PAC=30.
∵PC+BP=BC=30+30![]() ,
,
∴航行时间:(30+30![]() )÷30=1+
)÷30=1+![]() (小时).
(小时).
答:该渔船从B处开始航行(1+![]() )小时到达C处.
)小时到达C处.


科目:初中数学 来源: 题型:
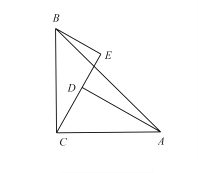
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE,垂足E,AD⊥CE, 垂足为 D,AD=2.5cm,BE=1.7cm,
(1).求证:△BCE≌△CAD
(2).求DE 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请认真观察图形,解答下列问题:
(1)根据图中条件,用两种方法表示两个阴影图形的面积的和(只需表示,不必化简);
(2)由(1),你能得到怎样的等量关系?请用等式表示;
(3)如果图中的a,b(a>b)满足a2+b2=53,ab=14,求:①![]() 的值;②a﹣b的值.
的值;②a﹣b的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,BD是一条对角线,点P在CD上(与点C,D不重合),连接AP,平移△ADP,使点D移动到点C,得到△BCQ,过点Q作QM⊥BD于M,连接AM,PM(如图1).

(1)判断AM与PM的数量关系与位置关系并加以证明;
(2)若点P在线段CD的延长线上,其它条件不变(如图2),(1)中的结论是否仍成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF∥AD,∠1=∠2,∠B=35°,将求∠BDG的过程填写完整。
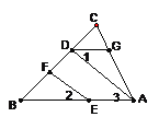
解: ∵EF∥AD,
∴∠2=____ (________________________________)
又∵∠1=∠2
∴∠1= ( 等量代换 )
∴DG∥_____ (___________________________________)
∴∠B+______=180°(___________________________)
∵∠B=35°
∴∠BDG =_______
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com