
【题目】请认真观察图形,解答下列问题:
(1)根据图中条件,用两种方法表示两个阴影图形的面积的和(只需表示,不必化简);
(2)由(1),你能得到怎样的等量关系?请用等式表示;
(3)如果图中的a,b(a>b)满足a2+b2=53,ab=14,求:①![]() 的值;②a﹣b的值.
的值;②a﹣b的值.

【答案】(1)、a2+b2或 (a+b)2﹣2ab;(2)、a2+b2=(a+b)2﹣2ab;(3)、①、![]() ;②、5.
;②、5.
【解析】
试题分析:(1)、阴影部分的面积等于两个小正方形的面积之和,同时也等于大正方形的面积减去两个小长方形的面积;(2)、根据面积相等得到等式;(3)、①根据题意求出a+b的值,然后将所求的分式进行通分得出答案;②根据已知求出![]() 的值,然后根据a>b得出答案.
的值,然后根据a>b得出答案.
试题解析:(1)、两个阴影图形的面积和可表示为:a2+b2或 (a+b)2﹣2ab;
(2)、a2+b2=(a+b)2﹣2ab;
(3)、∵a,b(a>b)满足a2+b2=53,ab=14,
∴①(a+b)2=a2+b2+2ab
=53+2×14=81 ∴a+b=±9, 又∵a>0,b>0,∴a+b=9.∴![]() =
=![]() =
=![]()
②∵![]() =53-2×14=25 又∵a>b>0,∴a﹣b=5,
=53-2×14=25 又∵a>b>0,∴a﹣b=5,


科目:初中数学 来源: 题型:
【题目】下面关于有理数的说法正确的是
A. 整数和分数统称为有理数
B. 正整数集合与负整数集合合在一起就构成整数集合
C. 有限小数和无限循环小数不是有理数
D. 正数、负数和零统称为有理数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的三个顶点位置如图所示.
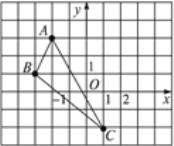
(1) 请画出△ABC关于y轴对称的△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点);(3分)
(2) 直接写出△A′B′C′三点的坐标:A′_________,B′__________,C′_________.(3分)
(3)求A B′的长。(4分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中一小岛有一个观测点A,某天上午观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.B处距离观测点30![]() 海里,若该渔船的速度为每小时30海里,问该渔船多长时间到达观测点A的北偏西60°方向上的C处?(计算结果用根号表示,不取近似值)
海里,若该渔船的速度为每小时30海里,问该渔船多长时间到达观测点A的北偏西60°方向上的C处?(计算结果用根号表示,不取近似值)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小乐玩猜牌游戏,小明手中有红桃、黑桃、梅花扑克牌共24张,其中红桃8张,黑桃是梅花的2倍少2张.
(1)黑桃 张,梅花 张 .
(2)小乐从小明手中任意抽取一张牌,抽到梅花的概率是多少?抽到哪种花样扑克牌的概率最大?最大概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,直线![]() 经过点(2,3)和(-1,-3),直线
经过点(2,3)和(-1,-3),直线![]() 经过原点,且与直线
经过原点,且与直线![]() 交于点P(-2,a).
交于点P(-2,a).
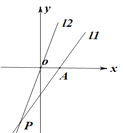
(1)求a的值.
(2)(-2,a)可看成怎样的二元一次方程组的解?
(3)设直线![]() 与x轴交于点A,你能求出△APO的面积吗?
与x轴交于点A,你能求出△APO的面积吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,四边形ABCD四个顶点的坐标分别为A(-2,0),B(-1,2),C(3,3),D(4, 0).
(1)画出四边形ABCD;
(2)把四边形ABCD向下平移4个单位长度,再向左平移2个单位长度得到四边形A′B′C′D′,画出四边形A′B′C′D′,并写出C′的坐标。
(3)求出四边形ABCD的面积。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com