Question

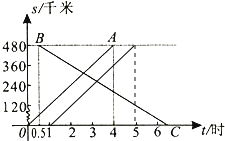
【题目】某客运公司有豪华和普通两种客车在甲、乙两市之间运营.已知每隔1h有一辆豪华客车从甲城开往乙城，如图所示，是第一辆豪华客车离开甲市的路程(km)与运行时间(h)的函数图像，是一辆从乙市开往甲市的普通客车距甲市的路程(km)与运行时间(h)的函数图像.请根据图中提供的信息，解答下列问题:

(1)点的横坐标0.5的意义是普通客车发车时间比第一辆豪华客车发车时间 ，点的纵坐标 480的意义是 .

(2)请你在原图中直接画出第二辆豪华客车离开甲市的路程(km)与运行时间(h)的函数图像;

(3)若普通客车的速度为80 km/h.

①求的函数表达式，并写出自变量的取值范围;

②求第二辆豪华客车出发后多长时间与普通客车相遇;

③写出这辆普通客车在行驶途中与迎面而来的相邻两辆豪华客车相遇的间隔时间.

Answer 1

【答案】(1) 晚0.5h ，甲乙两市相距480km；(2) 详见解析； (3) ①；②第二辆客车出发2.2h后与普通客车相遇；③间隔时间为0.6h.

【解析】

(1)直接根据图象回答即可.

(2)与OA平行，比第一辆豪华客车晚1小时出发.

(3) ①利用两点法代入BC点坐标即可求出解析式；
②写出第二辆豪华客车的函数解析式，与普通客车联立解方程组；
③求出与普通客车相遇的时间在上一问的基础上求差就可以．

(1) 点的横坐标0.5的意义是普通客车发车时间比第一辆豪华客车发车时间晚0.5 h, 点的纵坐标 480的意义是甲、乙两城相距480km.

故答案为：晚0.5 h，甲、乙两城相距480km.

(2)

(3)①设直线BC的解析式为s=kt+b，

∵B(0.5,480),C(6.5,0)，

∴

解得：

∴s=80t+520，

自变量t的取值范围是

②设直线MN的解析式为s=kt+b,

∵M(1,0),N(5,480)，

∴

解得

∴s=120t120.

由①可知直线BC解析式为s=80t+520，

∴120t120=80t+520，

解得t=3.2，

∴3.21=2.2.

答：第二辆豪华客车出发2.2h后与普通客车相遇。

③根据题意，普通客车的解析式为y=120t，

∴120t=52080t，

解得t=2.6h，

3.22.6=0.6小时(或36分钟).

故答案为：晚0.6h；甲、乙两城相距300km.