
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC的平分线交BC于点O,OC=1,以点O为圆心OC为半径作半圆.
(1)求证:AB为⊙O的切线;
(2)如果tan∠CAO= ![]() ,求cosB的值.
,求cosB的值.
【答案】
(1)
解:如图作OM⊥AB于M,
∵OA平分∠CAB,OC⊥AC,OM⊥AB,
∴OC=OM,
∴AB是⊙O的切线,
(2)
解:设BM=x,OB=y,则y2﹣x2=1 ①,
∵cosB= ![]() ,
,
∴ ![]() ,
,
∴x2+3x=y2+y ②,
由①②可以得到:y=3x﹣1,
∴(3x﹣1)2﹣x2=1,
∴x= ![]() ,y=
,y= ![]() ,
,
∴cosB= ![]() =
= ![]() .
.
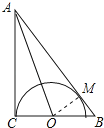
【解析】(1)如图作OM⊥AB于M,根据角平分线性质定理,可以证明OM=OC,由此即可证明.(2)设BM=x,OB=y,列方程组即可解决问题.本题考查切线的判定、勾股定理、三角函数等知识,解题的关键是记住圆心到直线的距离等于半径,这条直线就是圆的切线,学会设未知数列方程组解决问题,属于中考常考题型.
【考点精析】解答此题的关键在于理解切线的判定定理的相关知识,掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线,以及对锐角三角函数的定义的理解,了解锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数.


科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c经过A(﹣1,0),B(3,0)两点,与y轴相交于点C,该抛物线的顶点为点D
(1)求该抛物线的解析式及点D的坐标。
(2)连接AC,CD,BD,BC,设△AOC,△BOC,△BCD的面积分别为S1 , S2和S3 , 用等式表示S1 , S2 , S3之间的数量关系,并说明理由
(3)假设存在,设点M的坐标为(m,0),表示出MA的长,根据MN∥BC,得到比例式求出AN,根据△AMN∽△ACM,得到比例式求出m,得到点M的坐标,求出BC的解析式,根据MN∥BC,设直线MN的解析式,求解即可
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一个菱形绕着它的对角线的交点旋转90°,旋转前后的两个菱形构成一个“星形”(阴影部分),若菱形的一个内角为60°,边长为2,则该“星形”的面积是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月27日“丽水半程马拉松竞赛”在莲都举行,某运动员从起点万地广场西门出发,途经紫金大桥,沿比赛路线跑回中点万地广场西门.设该运动员离开起点的路程S(千米)与跑步时间t(分钟)之间的函数关系如图所示,其中从起点到紫金大桥的平均速度是0.3千米/分,用时35分钟,根据图象提供的信息,解答下列问题:
(1)求图中a的值;
(2)组委会在距离起点2.1千米处设立一个拍摄点C,该运动员从第一次经过C点到第二次经过C点所用的时间为68分钟.
①求AB所在直线的函数解析式;
②该运动员跑完赛程用时多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某客运公司有豪华和普通两种客车在甲、乙两市之间运营.已知每隔1h有一辆豪华客车从甲城开往乙城,如图所示,![]() 是第一辆豪华客车离开甲市的路程
是第一辆豪华客车离开甲市的路程![]() (km)与运行时间
(km)与运行时间![]() (h)的函数图像,
(h)的函数图像,![]() 是一辆从乙市开往甲市的普通客车距甲市的路程
是一辆从乙市开往甲市的普通客车距甲市的路程![]() (km)与运行时间
(km)与运行时间![]() (h)的函数图像.请根据图中提供的信息,解答下列问题:
(h)的函数图像.请根据图中提供的信息,解答下列问题:
(1)点![]() 的横坐标0.5的意义是普通客车发车时间比第一辆豪华客车发车时间 ,点
的横坐标0.5的意义是普通客车发车时间比第一辆豪华客车发车时间 ,点![]() 的纵坐标 480的意义是 .
的纵坐标 480的意义是 .
(2)请你在原图中直接画出第二辆豪华客车离开甲市的路程![]() (km)与运行时间
(km)与运行时间![]() (h)的函数图像;
(h)的函数图像;
(3)若普通客车的速度为80 km/h.
①求![]() 的函数表达式,并写出自变量
的函数表达式,并写出自变量![]() 的取值范围;
的取值范围;
②求第二辆豪华客车出发后多长时间与普通客车相遇;
③写出这辆普通客车在行驶途中与迎面而来的相邻两辆豪华客车相遇的间隔时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=2x2﹣3的图象是一条抛物线,下列关于该抛物线的说法,正确的是( )
A.抛物线开口向下
B.抛物线经过点(2,3)
C.抛物线的对称轴是直线x=1
D.抛物线与x轴有两个交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=a(x+1)2﹣3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C(0,﹣ ![]() ),顶点为D,对称轴与x轴交于点H,过点H的直线l交抛物线于P,Q两点,点Q在y轴的右侧.
),顶点为D,对称轴与x轴交于点H,过点H的直线l交抛物线于P,Q两点,点Q在y轴的右侧. 
(1)求a的值及点A,B的坐标;
(2)当直线l将四边形ABCD分为面积比为3:7的两部分时,求直线l的函数表达式;
(3)当点P位于第二象限时,设PQ的中点为M,点N在抛物线上,则以DP为对角线的四边形DMPN能否为菱形?若能,求出点N的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,随着我市铁路建设进程的加快,现规划从A地到B地有一条笔直的铁路通过,但在附近的C处有一大型油库,现测得油库C在A地的北偏东60°方向上,在B地的西北方向上,AB的距离为250( ![]() +1)米.已知在以油库C为中心,半径为200米的范围内施工均会对油库的安全造成影响.问若在此路段修建铁路,油库C是否会受到影响?请说明理由.
+1)米.已知在以油库C为中心,半径为200米的范围内施工均会对油库的安全造成影响.问若在此路段修建铁路,油库C是否会受到影响?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC和△DEF中,AB=AC,DE=DF,∠A=∠D.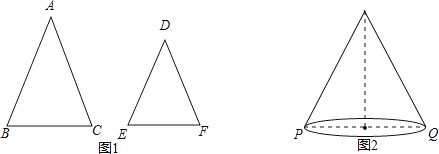
(1)求证: ![]() ;
;
(2)由(1)中的结论可知,等腰三角形ABC中,当顶角∠A的大小确定时,它的对边(即底边BC)与邻边(即腰AB或AC)的比值也就确定,我们把这个比值记作T(A),即T(A)= ![]() 的对边(底边)/
的对边(底边)/![]() 的领边(腰)=
的领边(腰)= ![]() ,如T(60°)=1.
,如T(60°)=1.
①理解巩固:T(90°)= , T(120°)= , 若α是等腰三角形的顶角,则T(α)的取值范围是;
②学以致用:如图2,圆锥的母线长为9,底面直径PQ=8,一只蚂蚁从点P沿着圆锥的侧面爬行到点Q,求蚂蚁爬行的最短路径长(精确到0.1).
(参考数据:T(160°)≈1.97,T(80°)≈1.29,T(40°)≈0.68)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com