
【题目】如图,随着我市铁路建设进程的加快,现规划从A地到B地有一条笔直的铁路通过,但在附近的C处有一大型油库,现测得油库C在A地的北偏东60°方向上,在B地的西北方向上,AB的距离为250( ![]() +1)米.已知在以油库C为中心,半径为200米的范围内施工均会对油库的安全造成影响.问若在此路段修建铁路,油库C是否会受到影响?请说明理由.
+1)米.已知在以油库C为中心,半径为200米的范围内施工均会对油库的安全造成影响.问若在此路段修建铁路,油库C是否会受到影响?请说明理由.
【答案】解:过点C作CD⊥AB于D,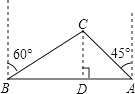
∴AD=CDcot45°=CD,
BD=CDcot30°= ![]() CD,
CD,
∵BD+AD=AB=250( ![]() +1)(米),
+1)(米),
即 ![]() CD+CD=250(
CD+CD=250( ![]() +1),
+1),
∴CD=250,
250米>200米.
答:在此路段修建铁路,油库C是不会受到影响
【解析】根据题意,在△ABC中,∠ABC=30°,∠BAC=45°,AB=250( ![]() +1)米,是否受到影响取决于C点到AB的距离,因此求C点到AB的距离,作CD⊥AB于D点.此题考查了解直角三角形及勾股定理的应用,用到的知识点是方向角,关键是根据题意画出图形,作出辅助线,构造直角三角形,“化斜为直”是解三角形的基本思路,常需作垂线(高),原则上不破坏特殊角(30°、45°、60°).
+1)米,是否受到影响取决于C点到AB的距离,因此求C点到AB的距离,作CD⊥AB于D点.此题考查了解直角三角形及勾股定理的应用,用到的知识点是方向角,关键是根据题意画出图形,作出辅助线,构造直角三角形,“化斜为直”是解三角形的基本思路,常需作垂线(高),原则上不破坏特殊角(30°、45°、60°).


 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】从﹣3,﹣1, ![]() ,1,3这五个数中,随机抽取一个数,记为a,若数a使关于x的不等式组
,1,3这五个数中,随机抽取一个数,记为a,若数a使关于x的不等式组  无解,且使关于x的分式方程
无解,且使关于x的分式方程 ![]() ﹣
﹣ ![]() =﹣1有整数解,那么这5个数中所有满足条件的a的值之和是( )
=﹣1有整数解,那么这5个数中所有满足条件的a的值之和是( )
A.﹣3
B.﹣2
C.﹣ ![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC的平分线交BC于点O,OC=1,以点O为圆心OC为半径作半圆.
(1)求证:AB为⊙O的切线;
(2)如果tan∠CAO= ![]() ,求cosB的值.
,求cosB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标xOy中,正比例函数y=kx的图象与反比例函数y= ![]() 的图象都经过点A(2,﹣2).
的图象都经过点A(2,﹣2). 
(1)分别求这两个函数的表达式;
(2)将直线OA向上平移3个单位长度后与y轴交于点B,与反比例函数图象在第四象限内的交点为C,连接AB,AC,求点C的坐标及△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线m:y=ax2﹣6ax+c(a>0)的顶点A在x轴上,并过点B(0,1),直线n:y=﹣ ![]() x+
x+ ![]() 与x轴交于点D,与抛物线m的对称轴l交于点F,过B点的直线BE与直线n相交于点E(﹣7,7).
与x轴交于点D,与抛物线m的对称轴l交于点F,过B点的直线BE与直线n相交于点E(﹣7,7).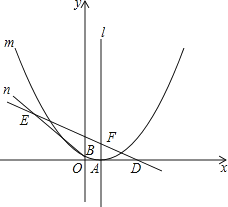
(1)求抛物线m的解析式;
(2)P是l上的一个动点,若以B,E,P为顶点的三角形的周长最小,求点P的坐标;
(3)抛物线m上是否存在一动点Q,使以线段FQ为直径的圆恰好经过点D?若存在,求点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y=﹣x+1与x轴,y轴分别交于A,B两点,点P,Q是直线l上的两个动点,且点P在第二象限,点Q在第四象限,∠POQ=135°.
(1)求△AOB的周长;
(2)设AQ=t>0,试用含t的代数式表示点P的坐标;
(3)当动点P,Q在直线l上运动到使得△AOQ与△BPO的周长相等时,记tan∠AOQ=m,若过点A的二次函数y=ax2+bx+c同时满足以下两个条件:
①6a+3b+2c=0;
②当m≤x≤m+2时,函数y的最大值等于 ![]() ,求二次项系数a的值.
,求二次项系数a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com